Distributions
Associations, correlation, PCA
MADS6
Wednesday, 11 March 2026
Session aims
Learning objectives
- Exploring a single distribution
- Associations
- Correlation plots
- Principal component analysis
Exploratory plots
We aim to find a basis - No lables and titles
Material
Chapter Statistical summaries in ggplot2: Elegant Graphics for Data Analysis (3e)
Consult the books for reference
We can only cover a fraction in class!
What are we visualising?
Amounts
x-y relationships
Trends
Proportions
Distributions
Uncertainty
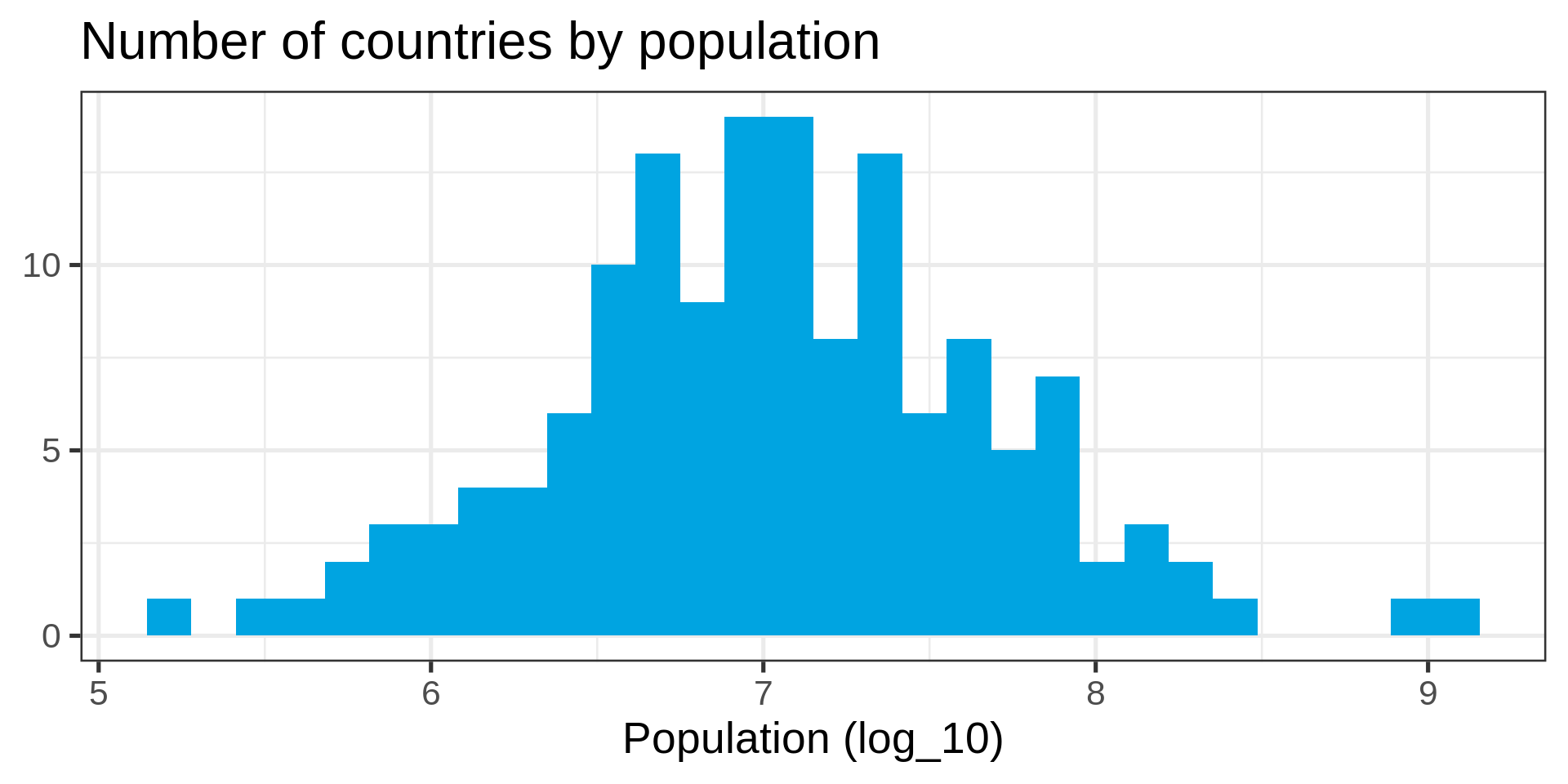
Distributions
Many distributions are not “normal”
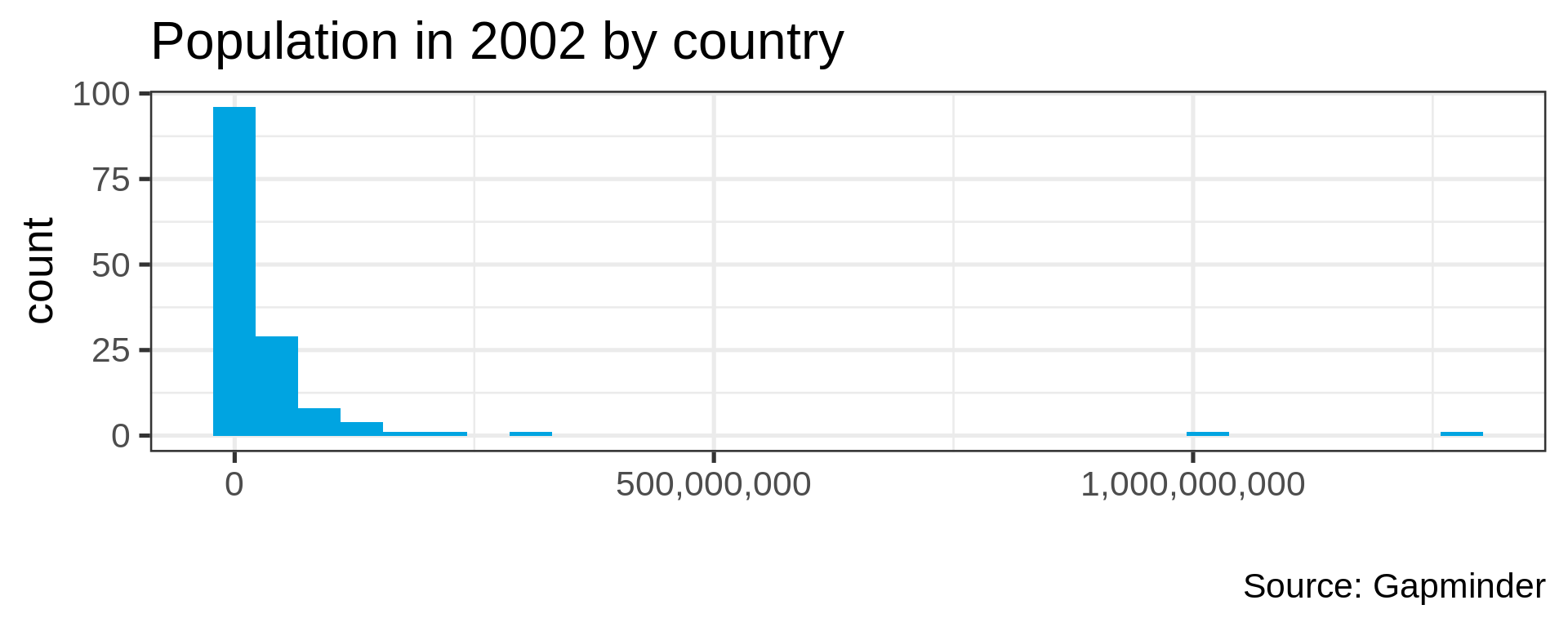
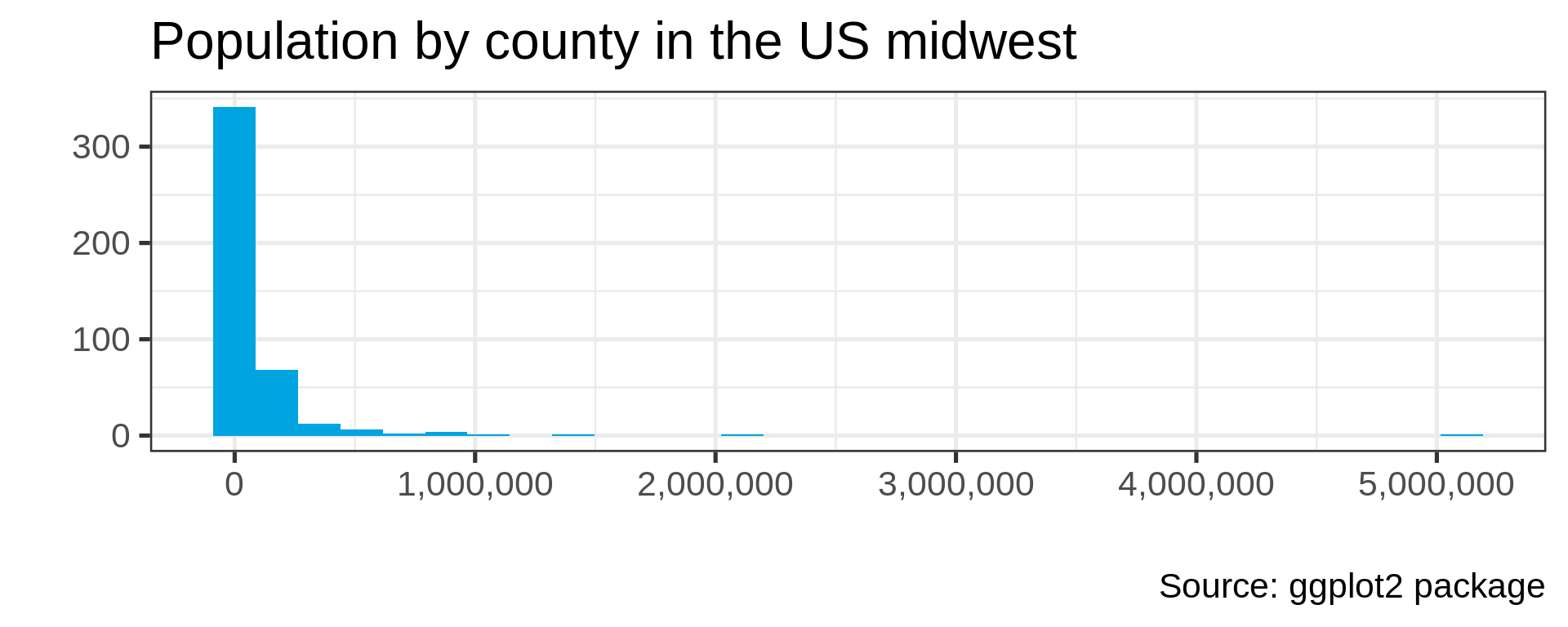
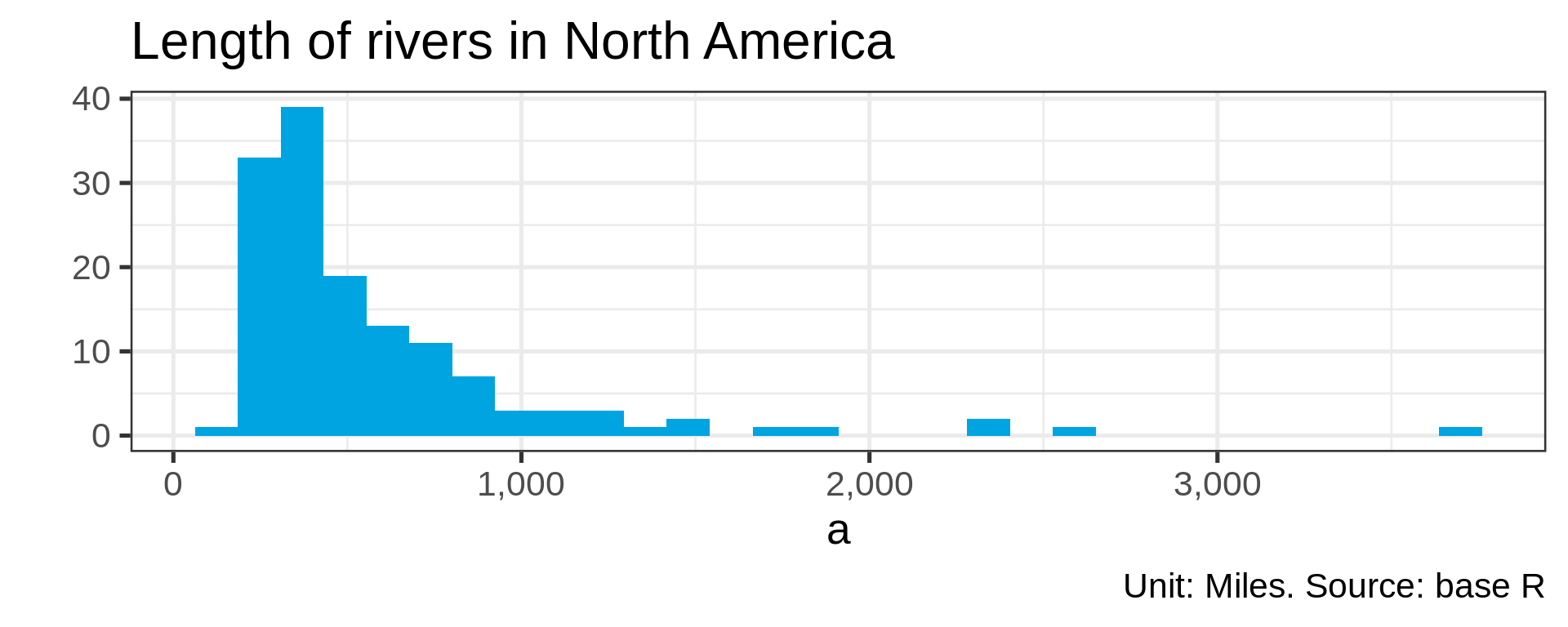
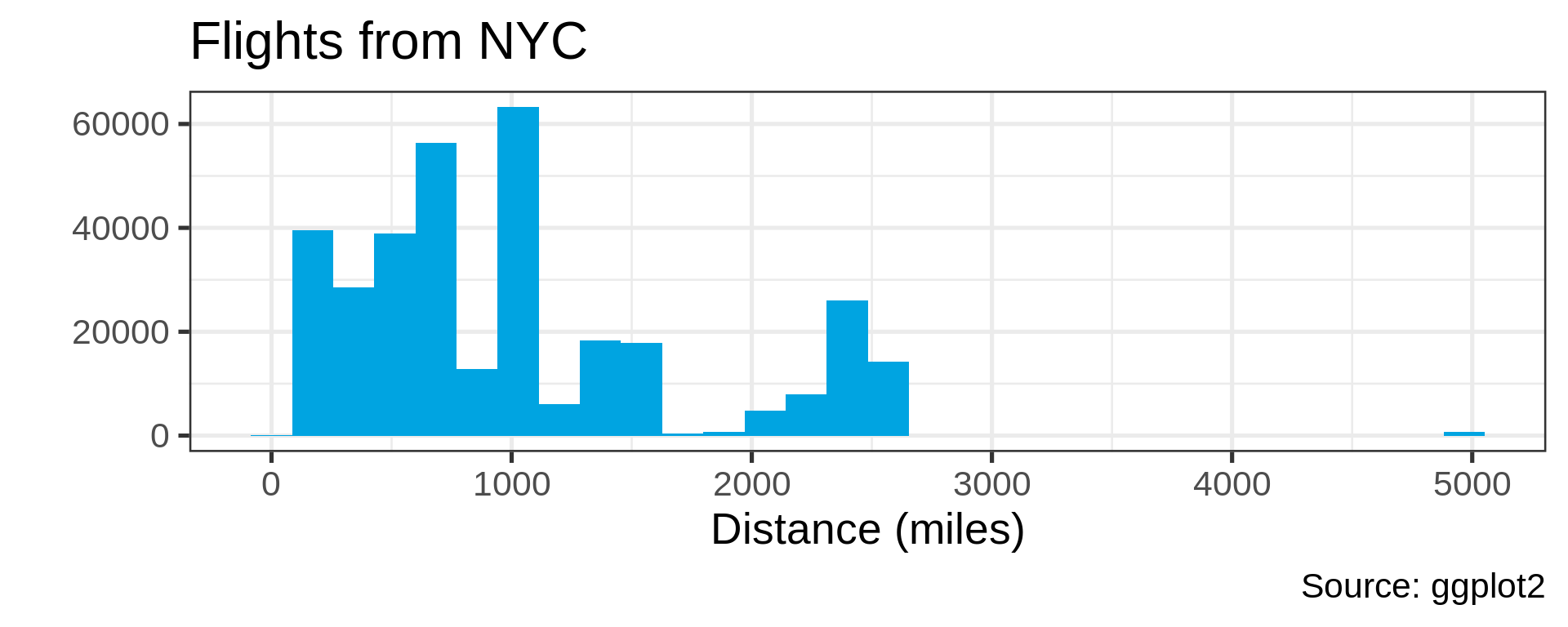
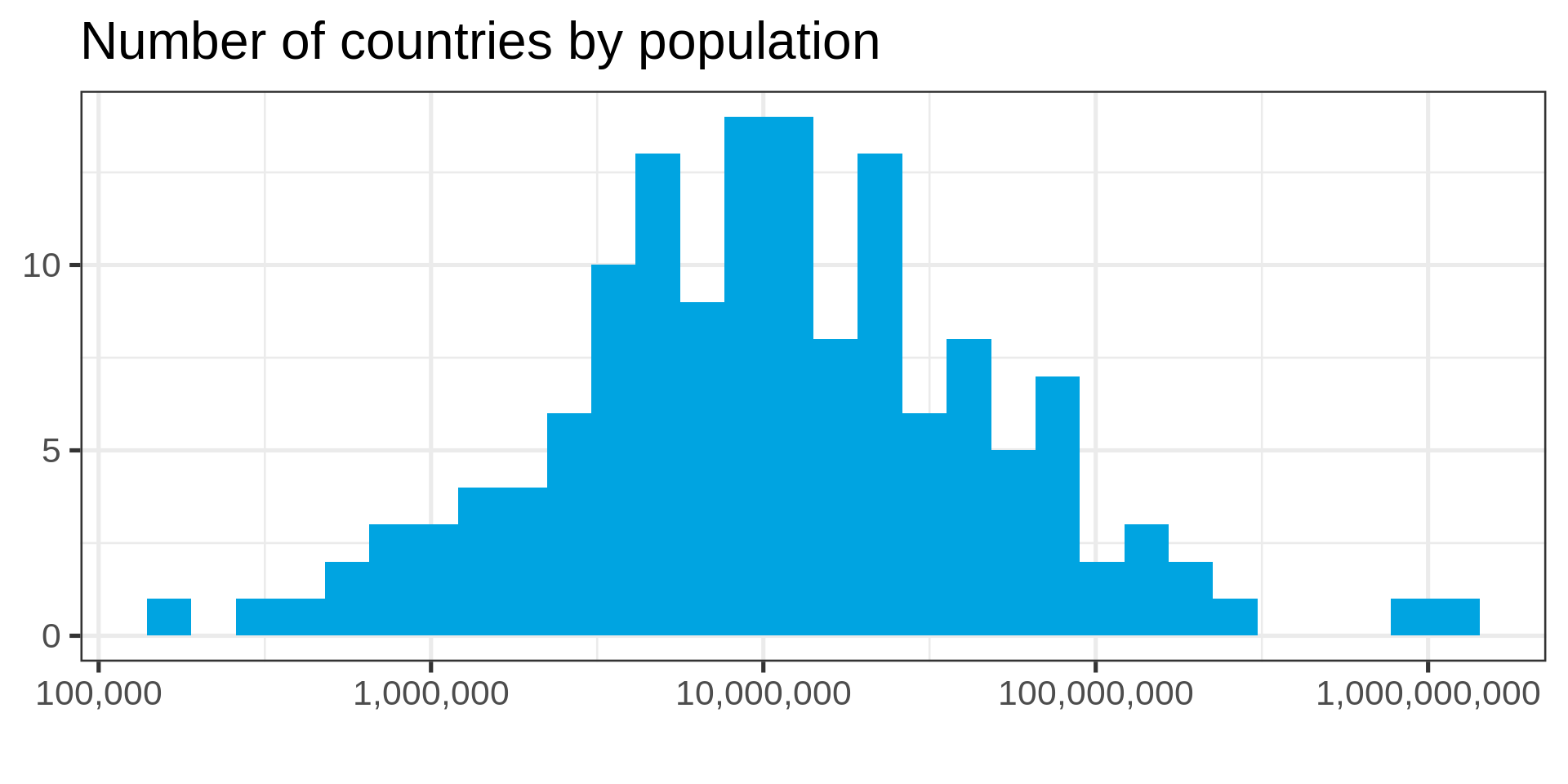
Power law distributions
- Common in natural data with network characteristic
Also not so normal
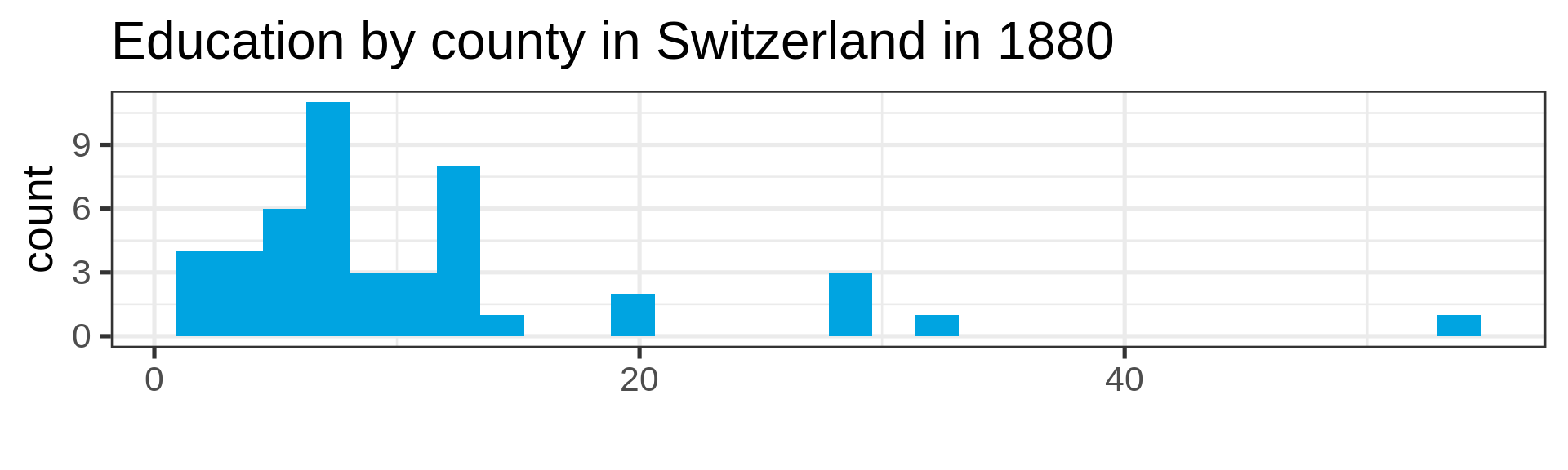
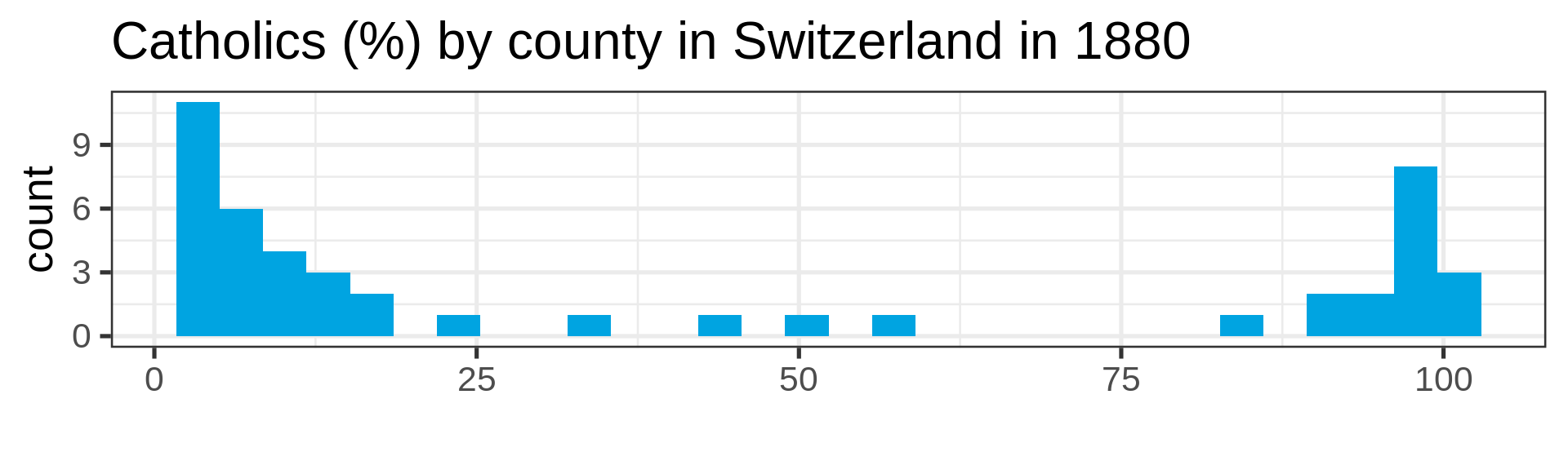
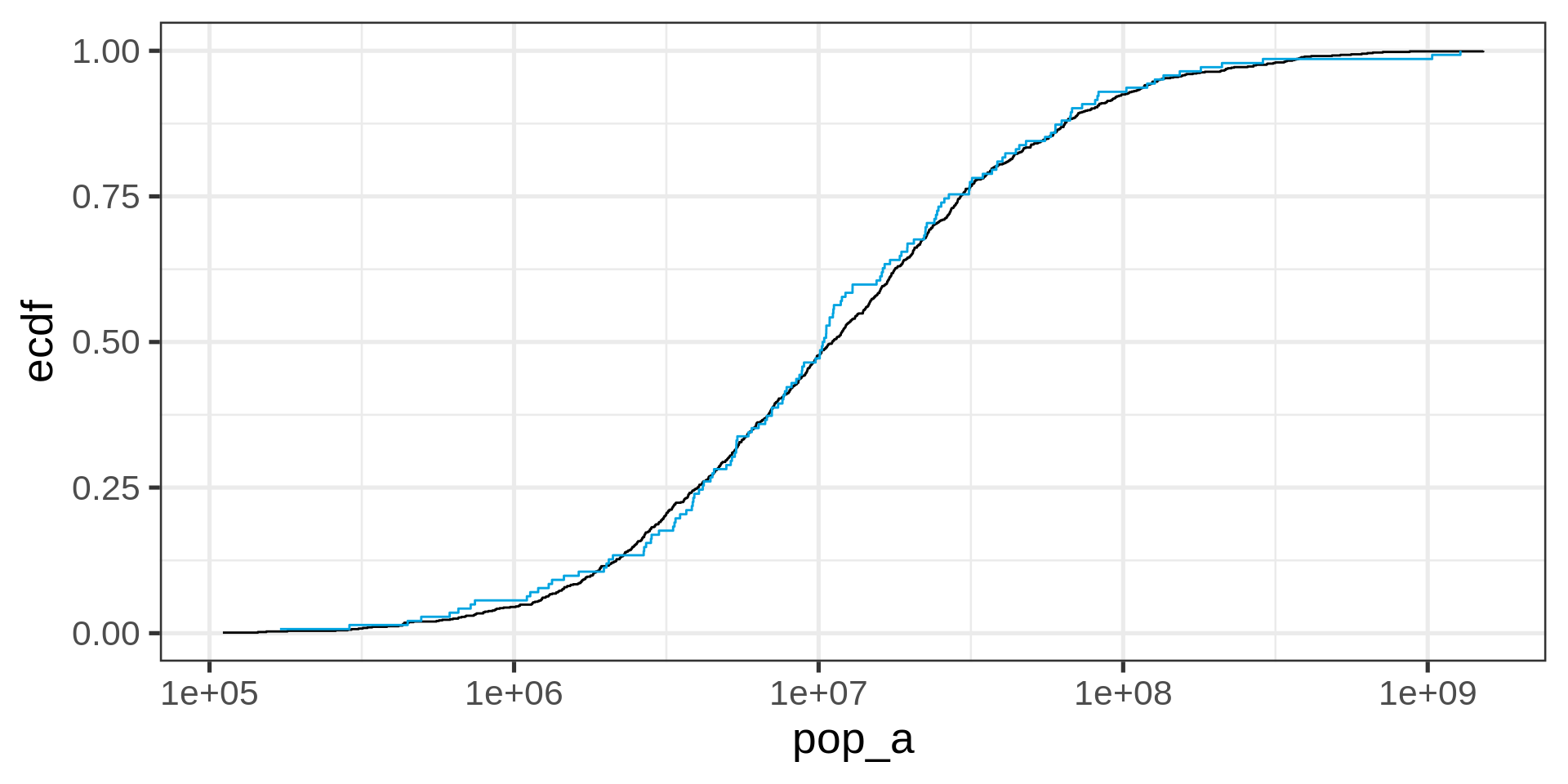
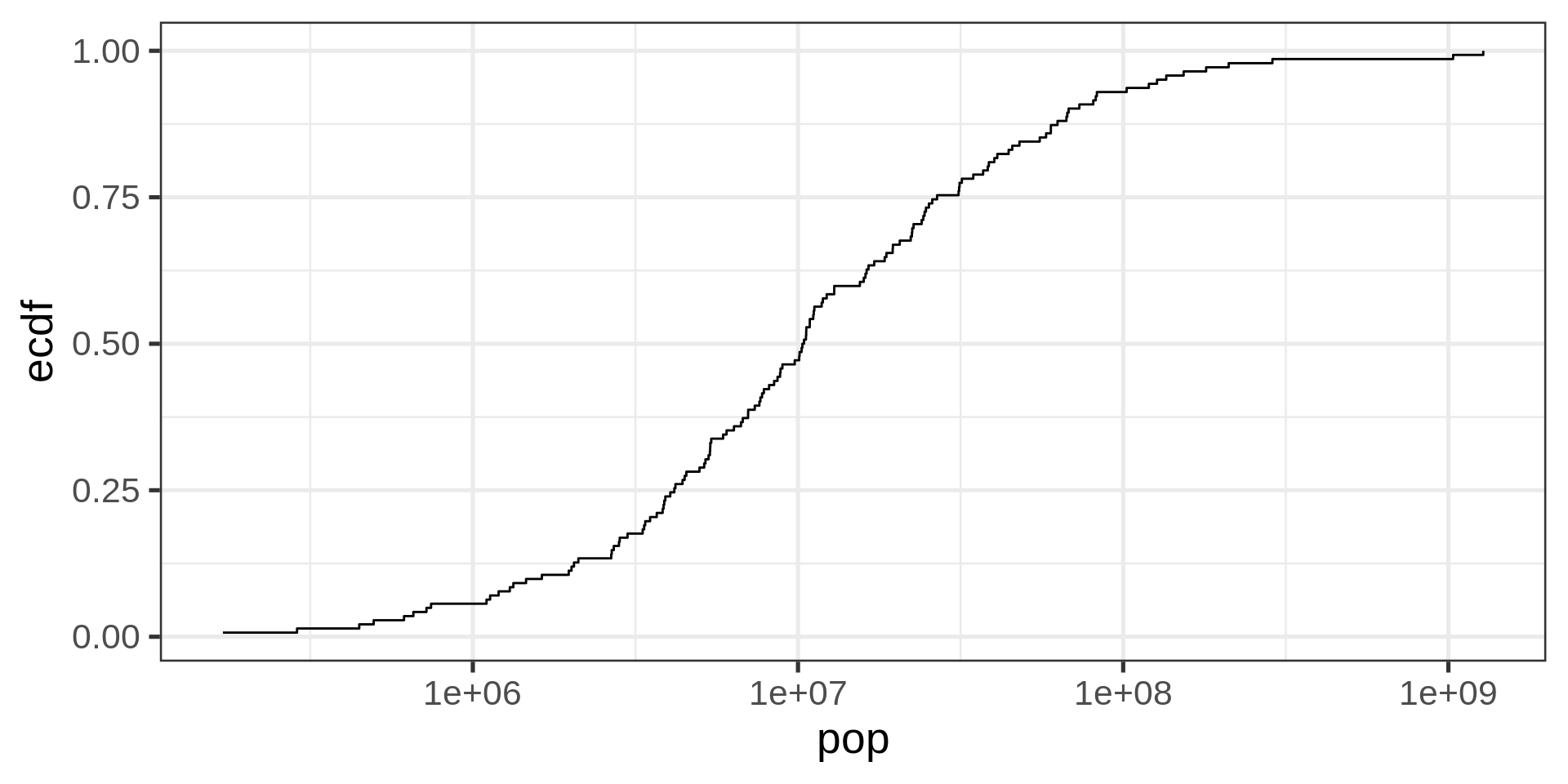
Empirical cumulative distribution functions
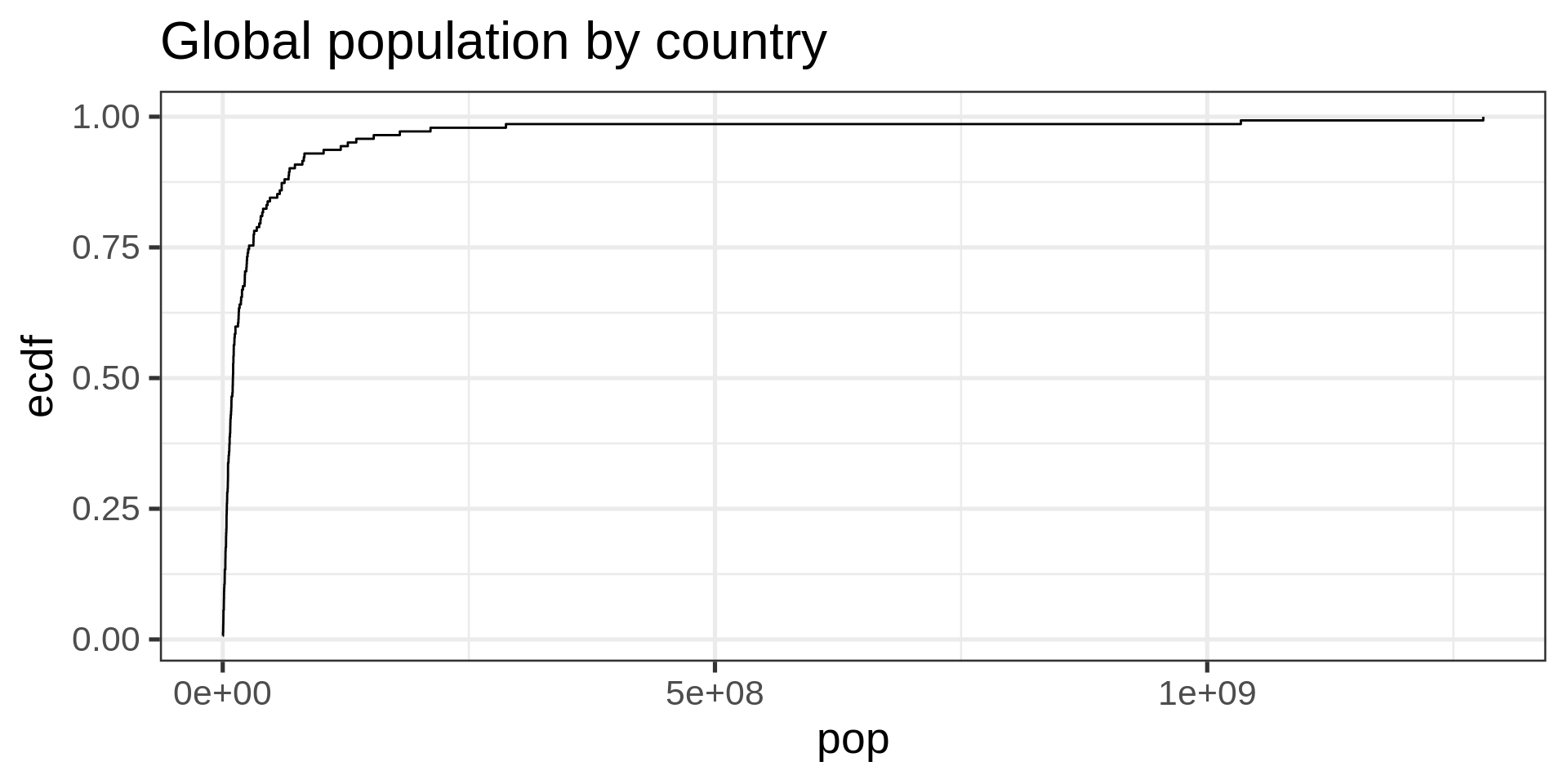
ECDF
No tuning parameter, possibly harder to interpret than a histogram
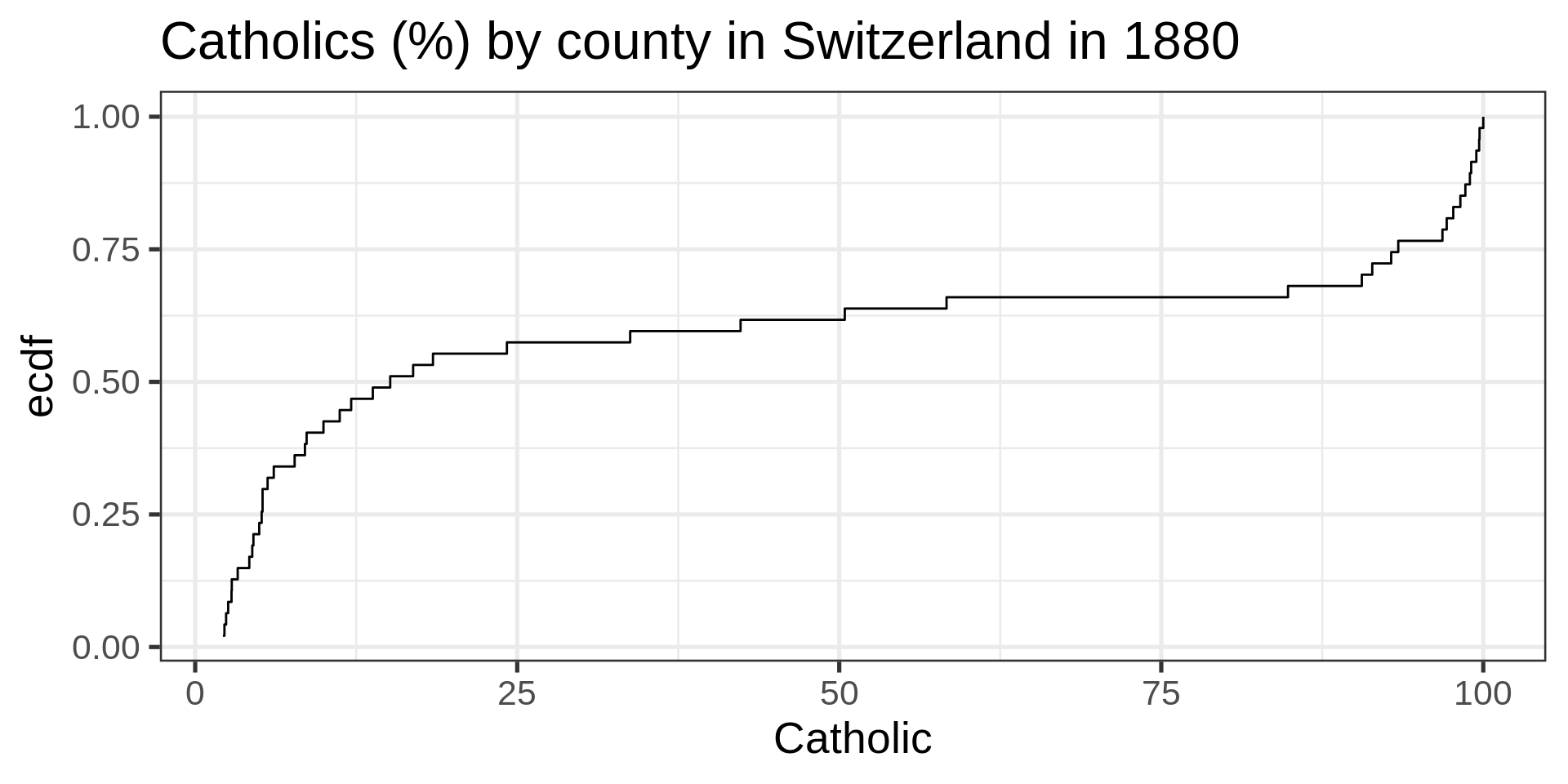
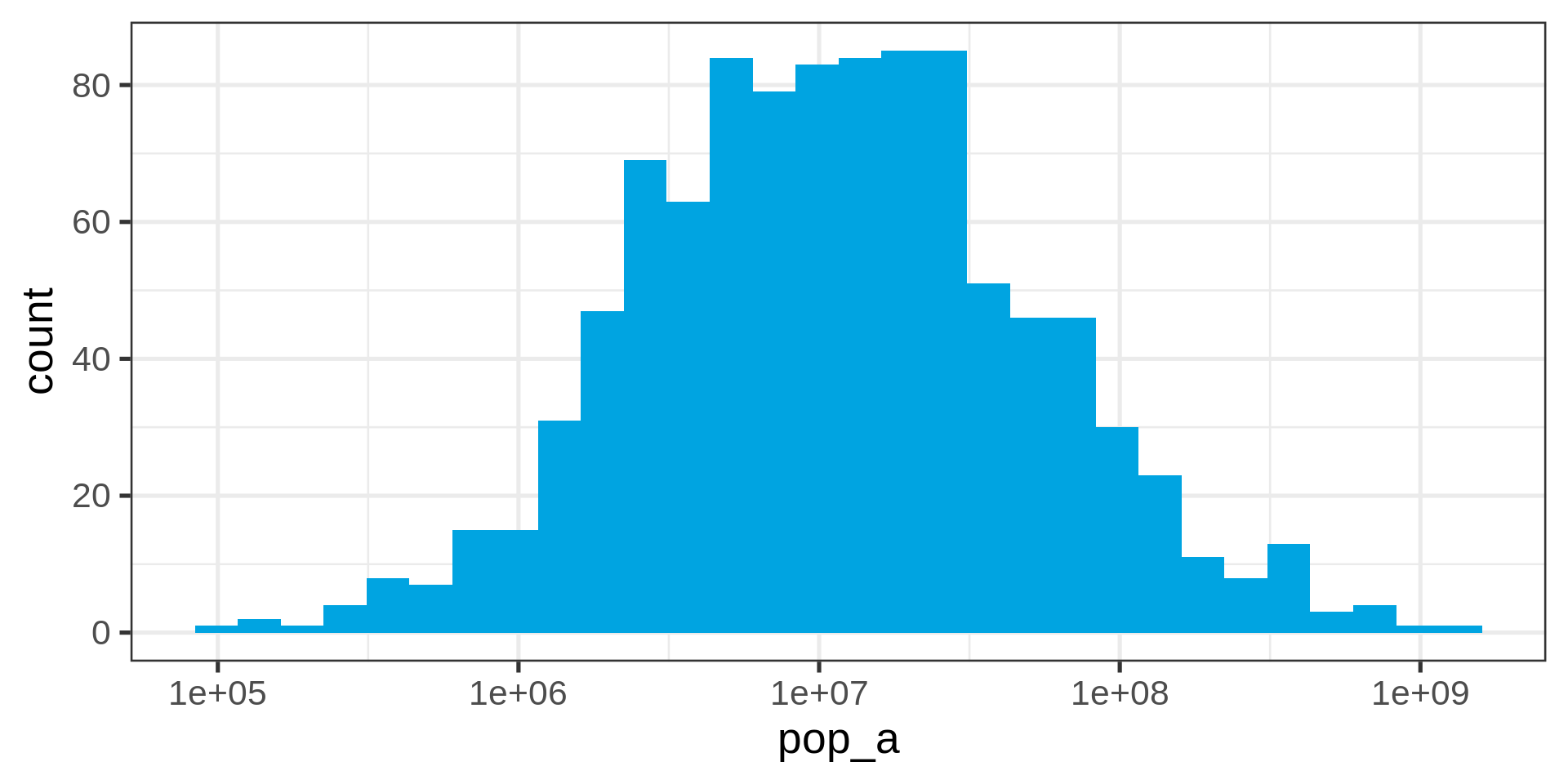
Log-transform
Tip
Use the log-transform in your plotting library. Don’t require your audience to compute!
Transformed ECDF
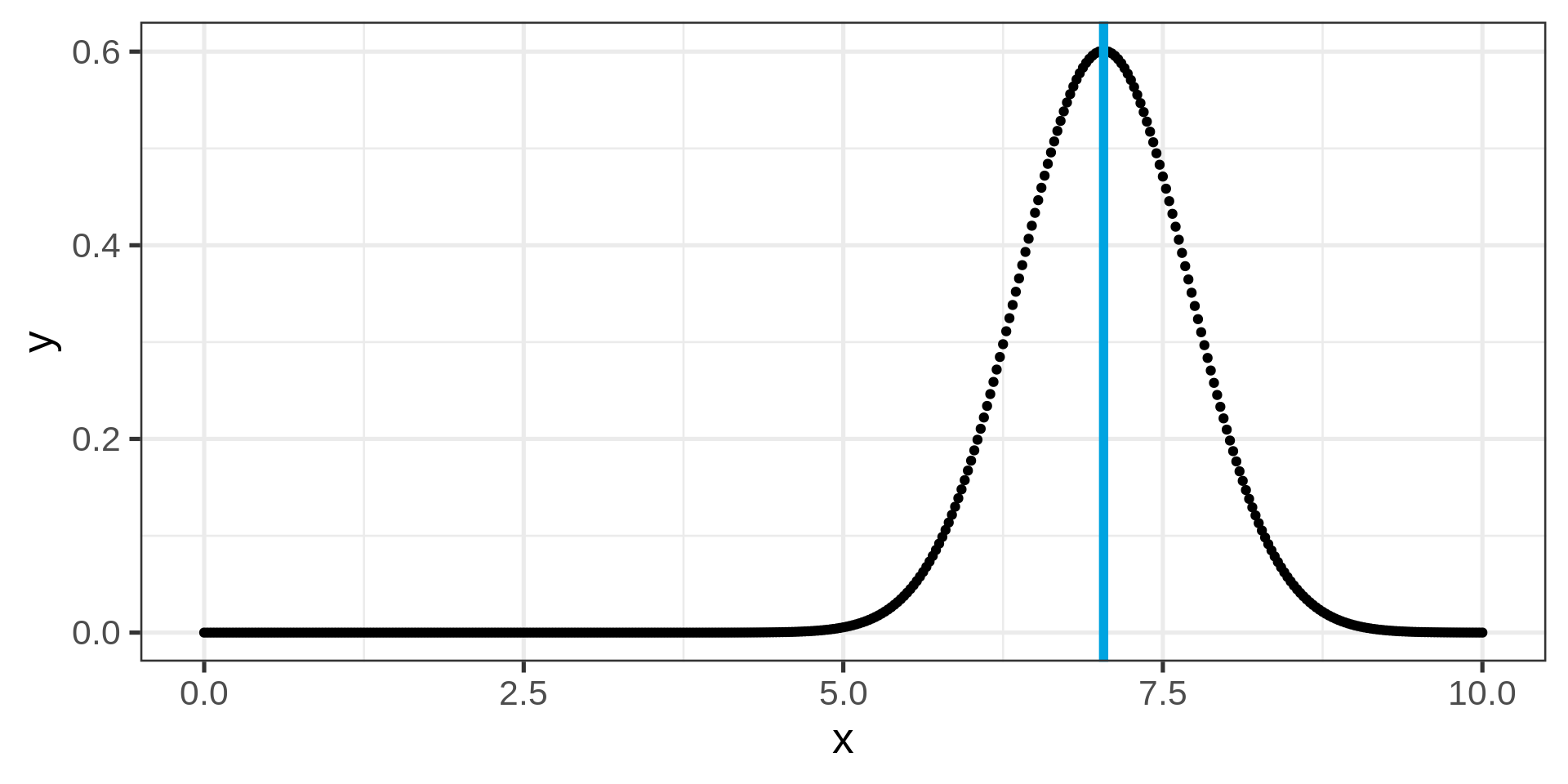
Plotting a normal distribution
A randomized histogram
Overlaying empirical and theoretical distribution
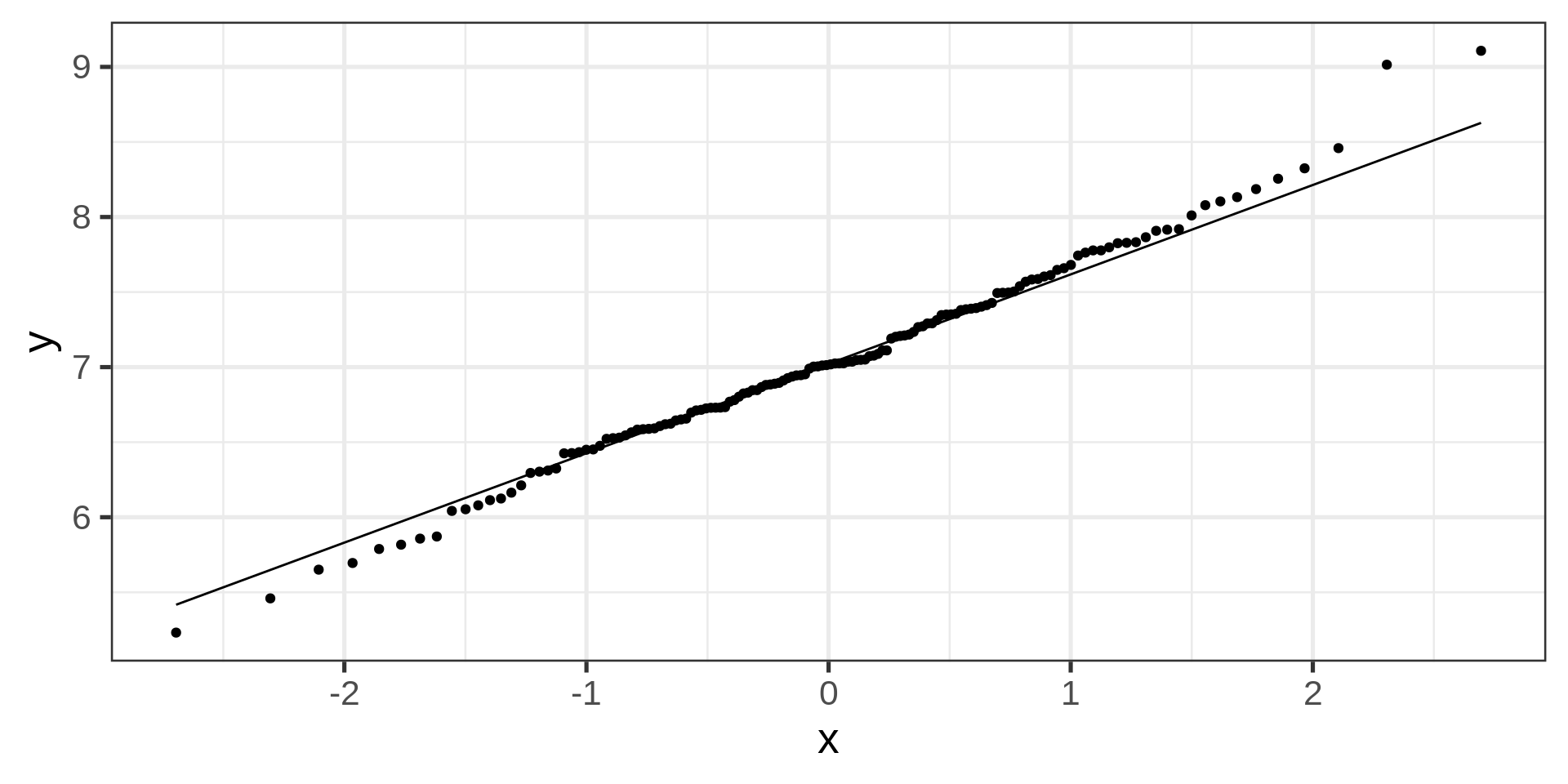
Quantile-quantile plot
Displaying many distributions
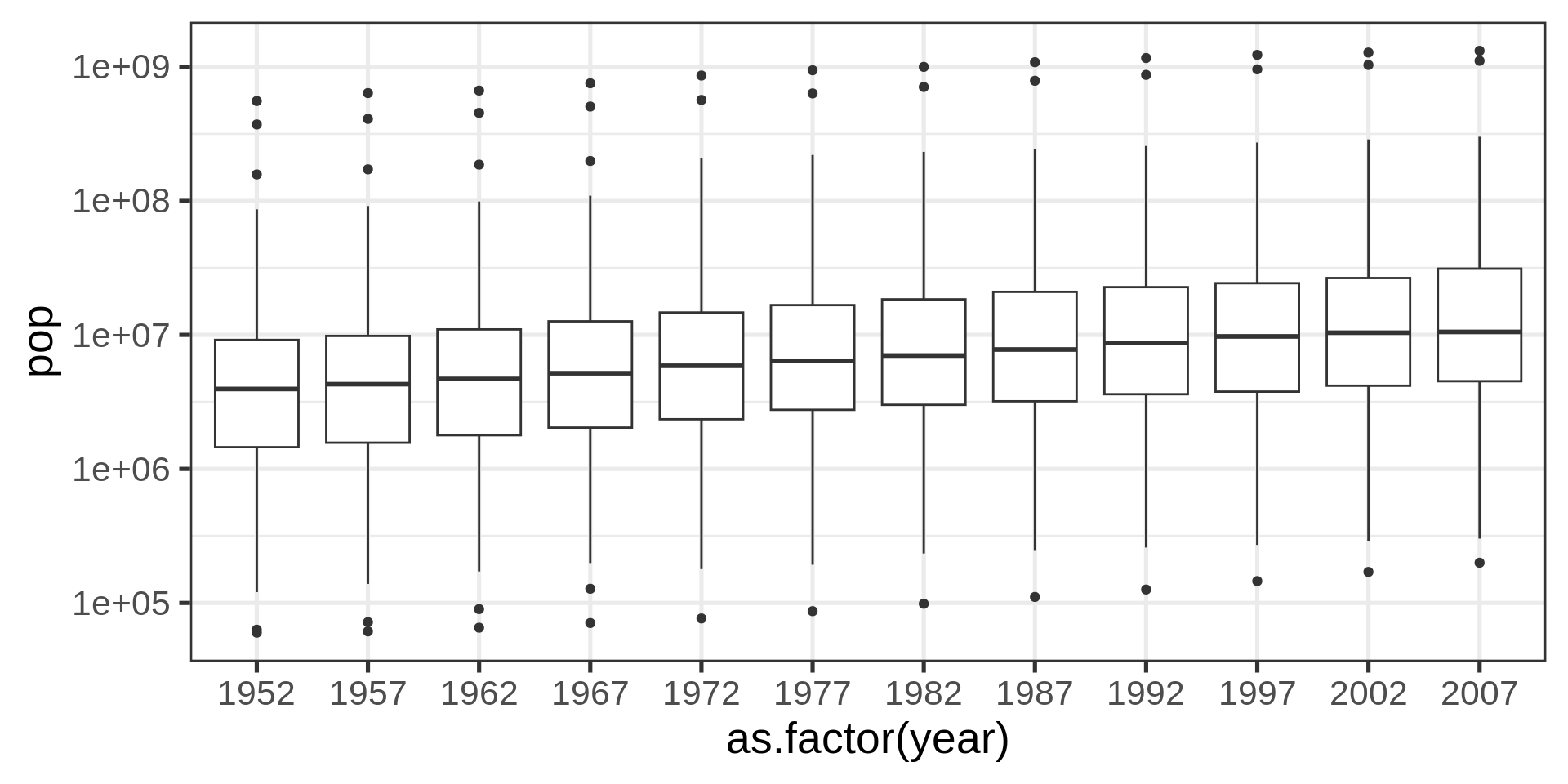
Boxplots
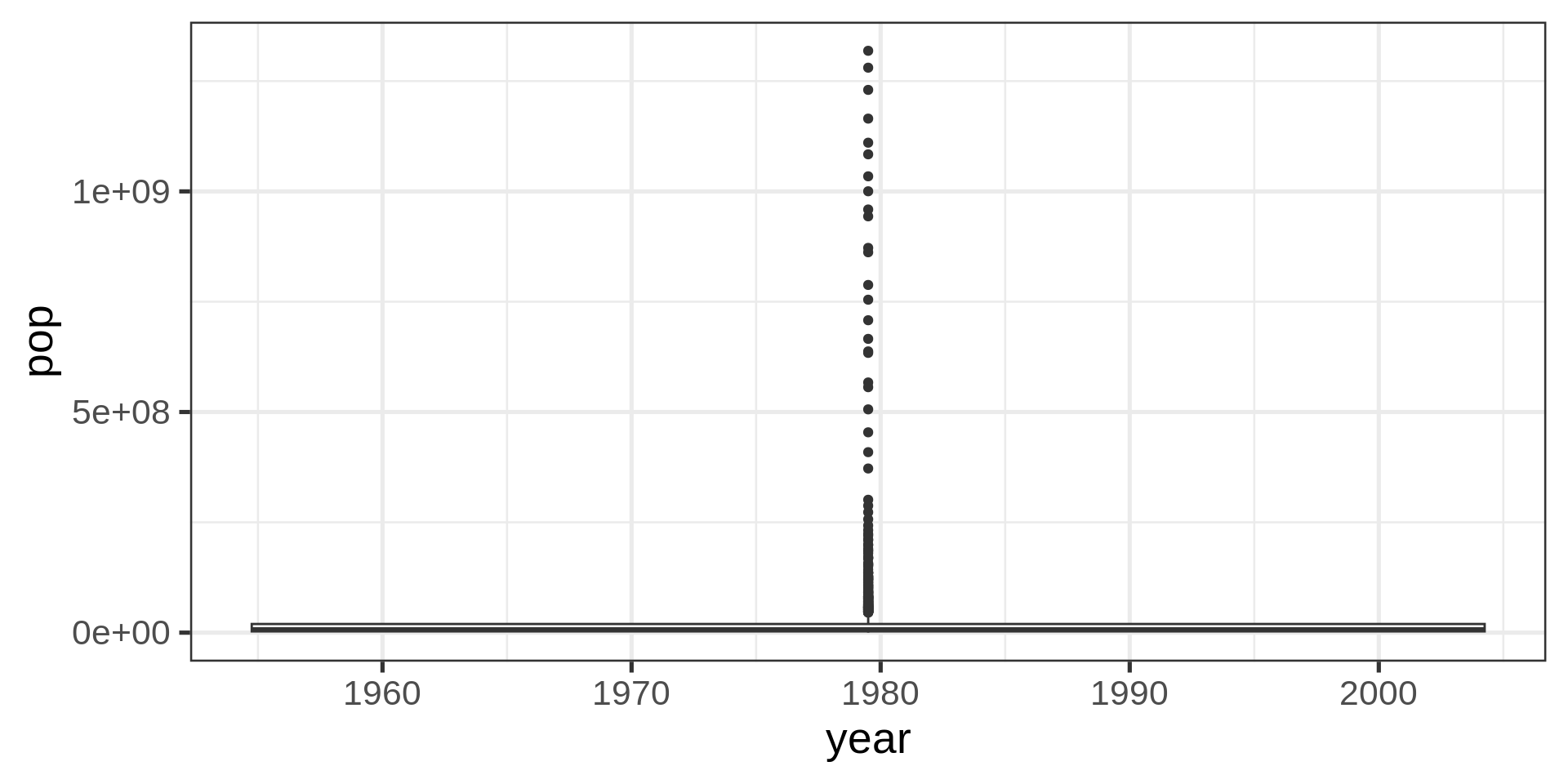
What are we missing?
Rows: 1,704
Columns: 6
$ country <fct> "Afghanistan", "Afghanistan", "Afghanistan", "Afghanistan", …
$ continent <fct> Asia, Asia, Asia, Asia, Asia, Asia, Asia, Asia, Asia, Asia, …
$ year <int> 1952, 1957, 1962, 1967, 1972, 1977, 1982, 1987, 1992, 1997, …
$ lifeExp <dbl> 28.801, 30.332, 31.997, 34.020, 36.088, 38.438, 39.854, 40.8…
$ pop <int> 8425333, 9240934, 10267083, 11537966, 13079460, 14880372, 12…
$ gdpPercap <dbl> 779.4453, 820.8530, 853.1007, 836.1971, 739.9811, 786.1134, …Year as date
With factors
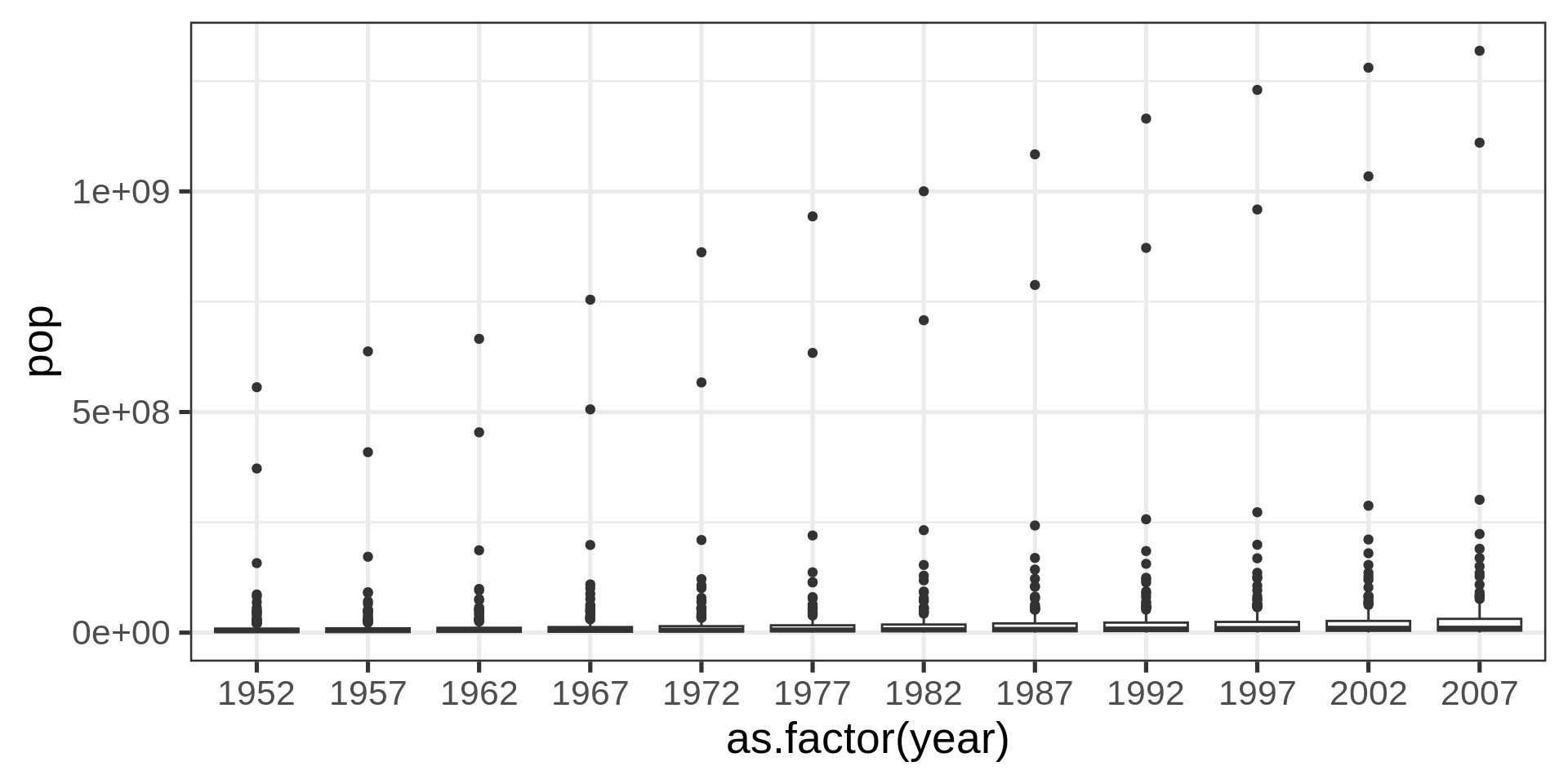
Better with transform
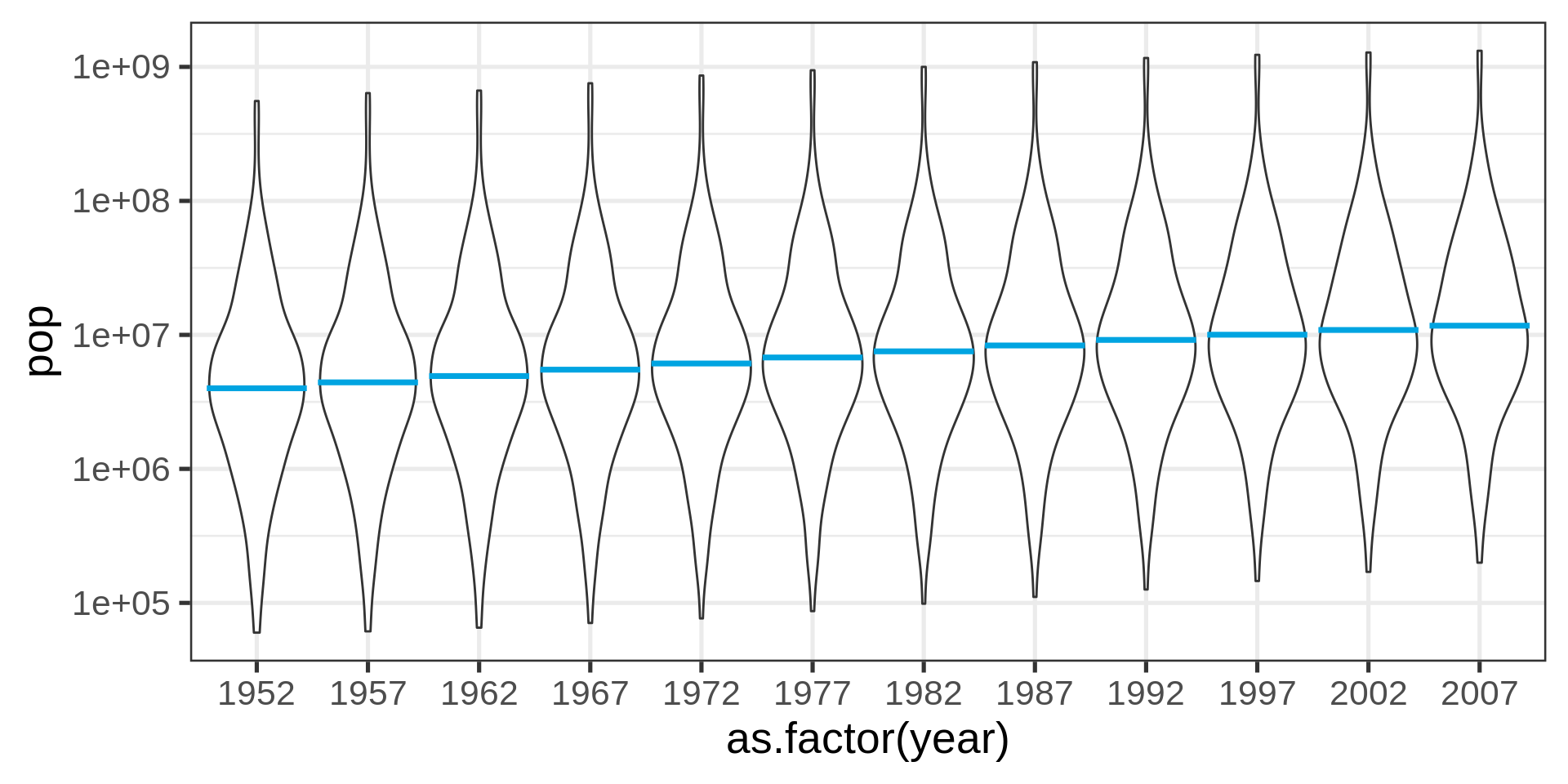
Even better?
Beeswarm plot
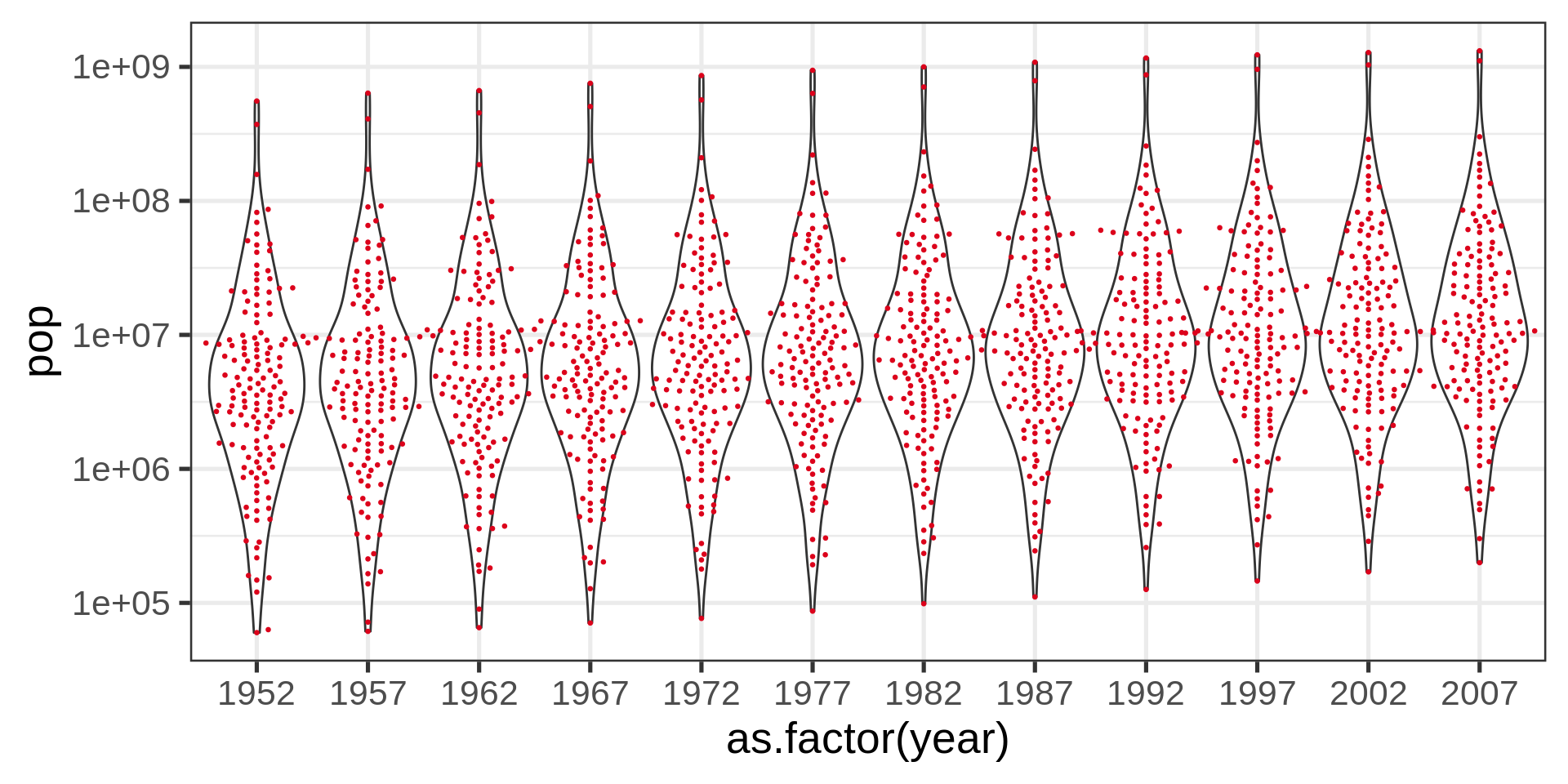
Red dots
Red color plots in the lecture material represent undesirable solutions to the plotting problem.
Ridge plot (densities)
library(ggridges)
gapminder |>
# filtering self-join for countries with
# less than 10M people in 1952
semi_join(gapminder |>
filter(year == 1952,
pop < 10000000) |>
select(country), join_by(country)) |>
ggplot(aes(y = as.factor(year), x= pop)) +
geom_density_ridges(fill = "#CDF6FF",
color = "#00a4e1") +
scale_x_sqrt()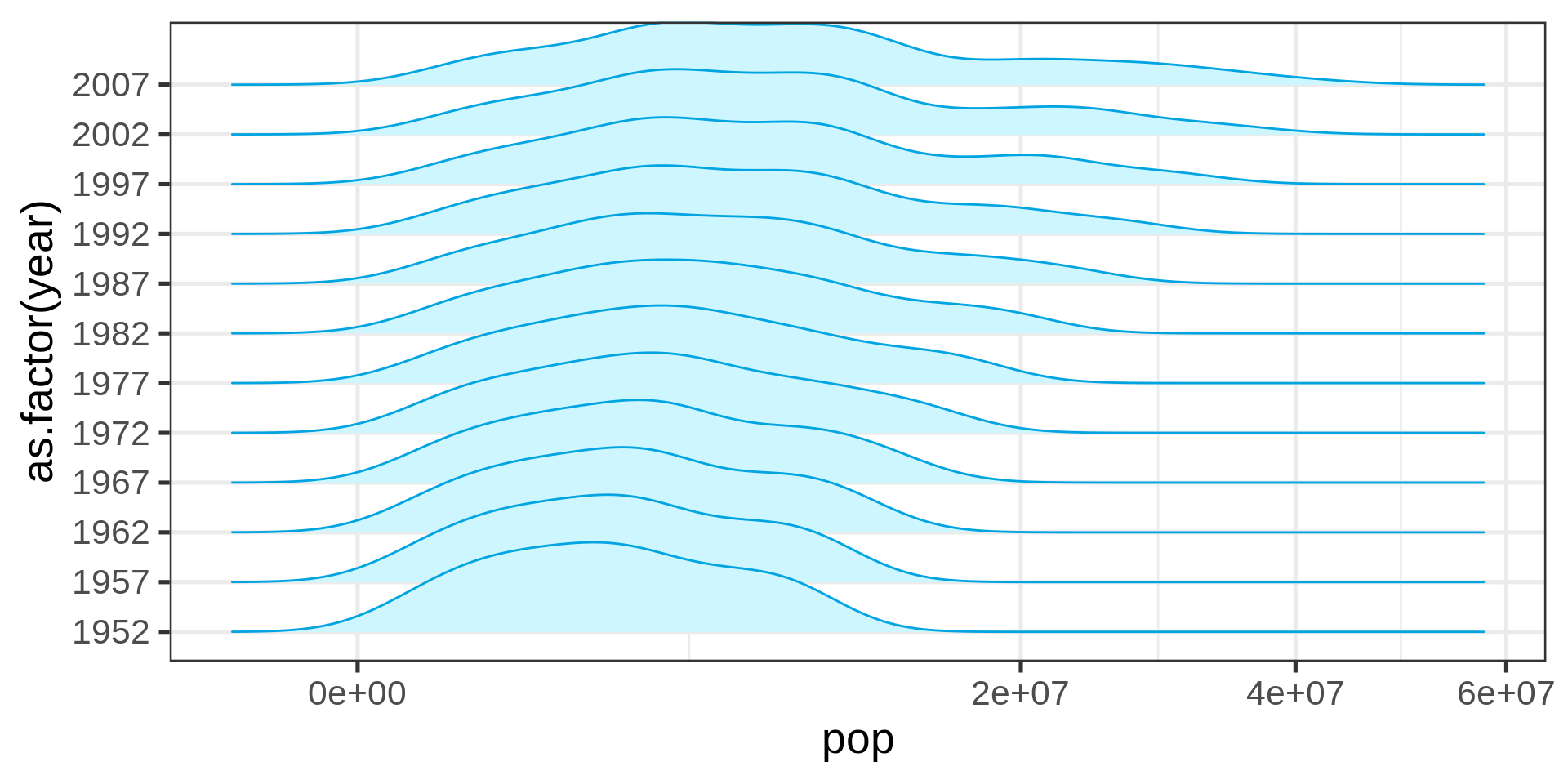
Ridge plots are a convenient shorthand for multiple distributions
The overlap can be controlled.
Two and more related variables
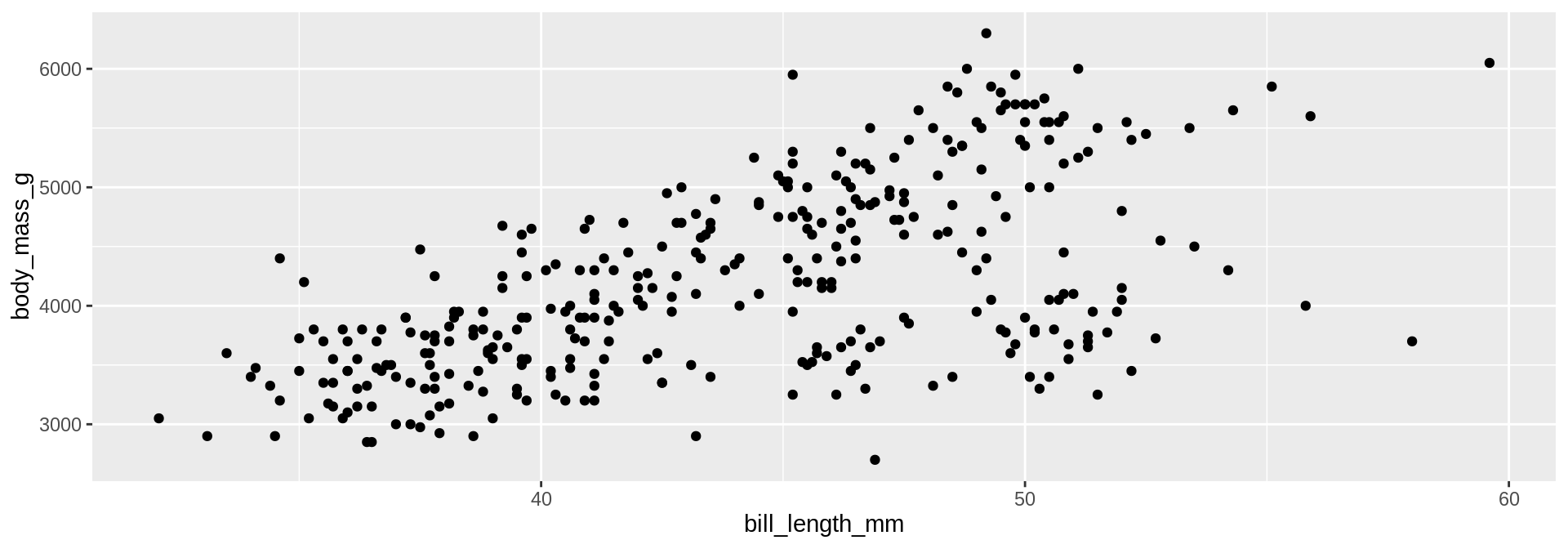
Scatter plot
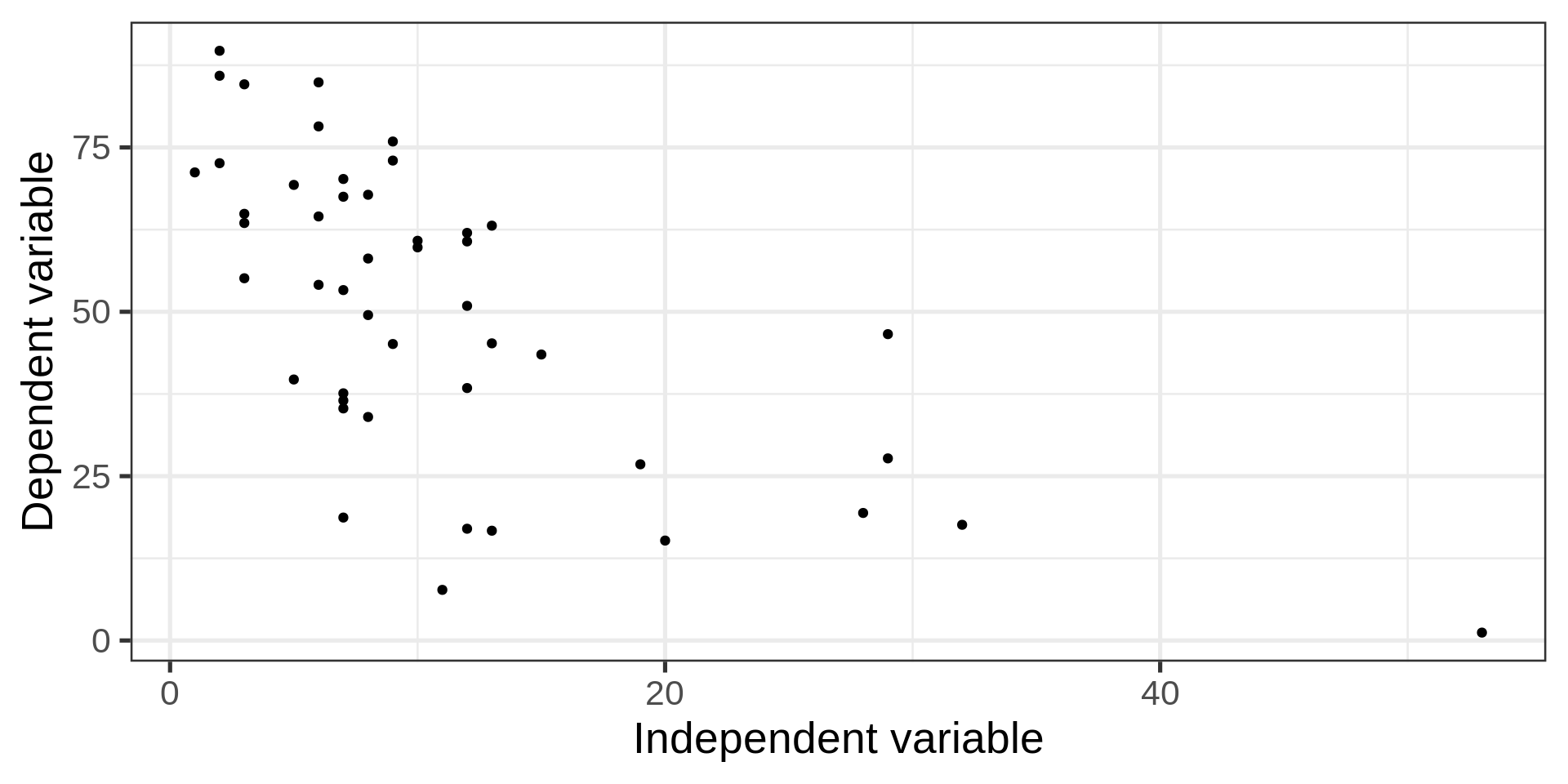
Back to the penguins
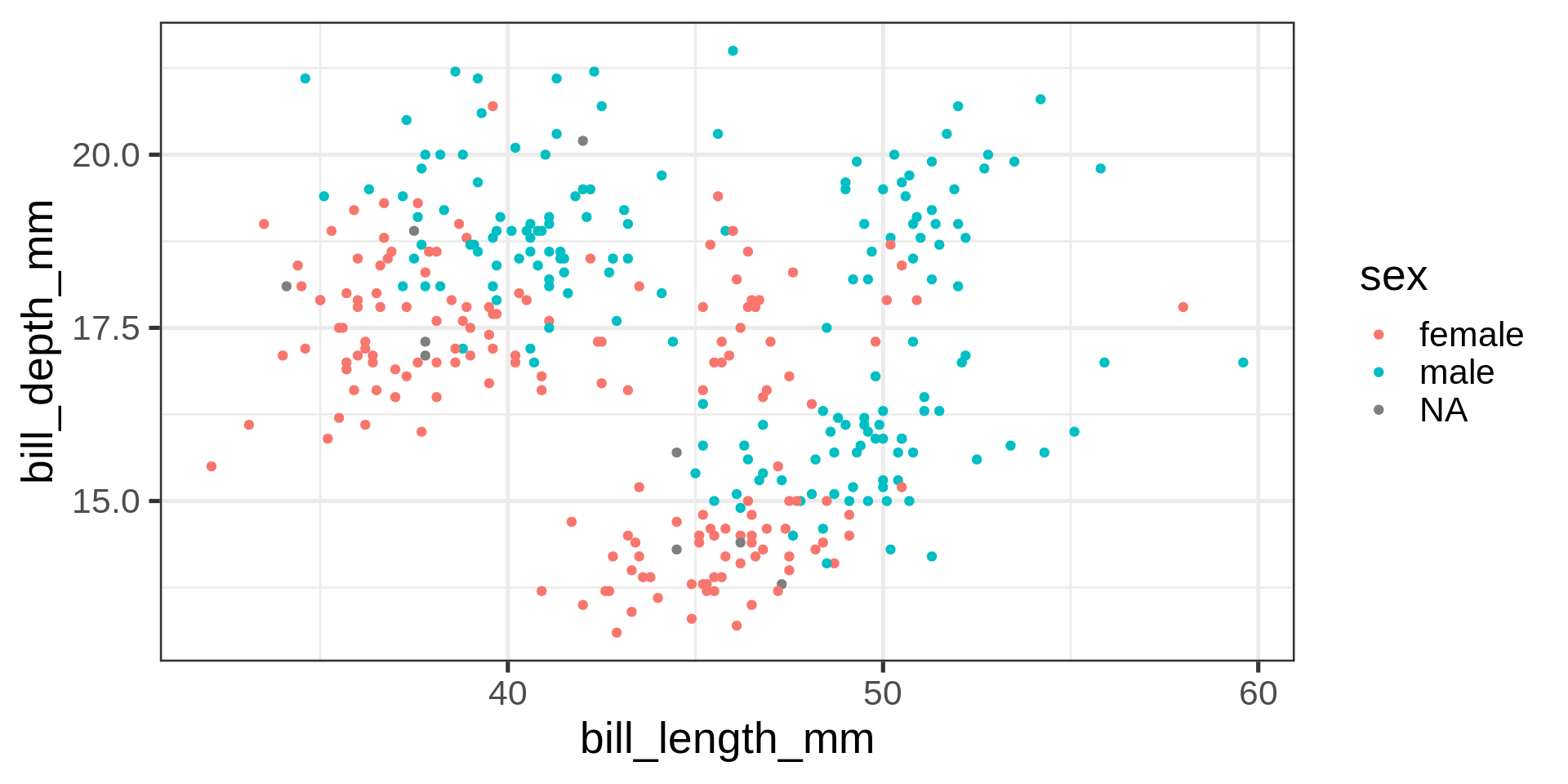
How to add bodymass and flipper length to this plot?
Adding another dimension
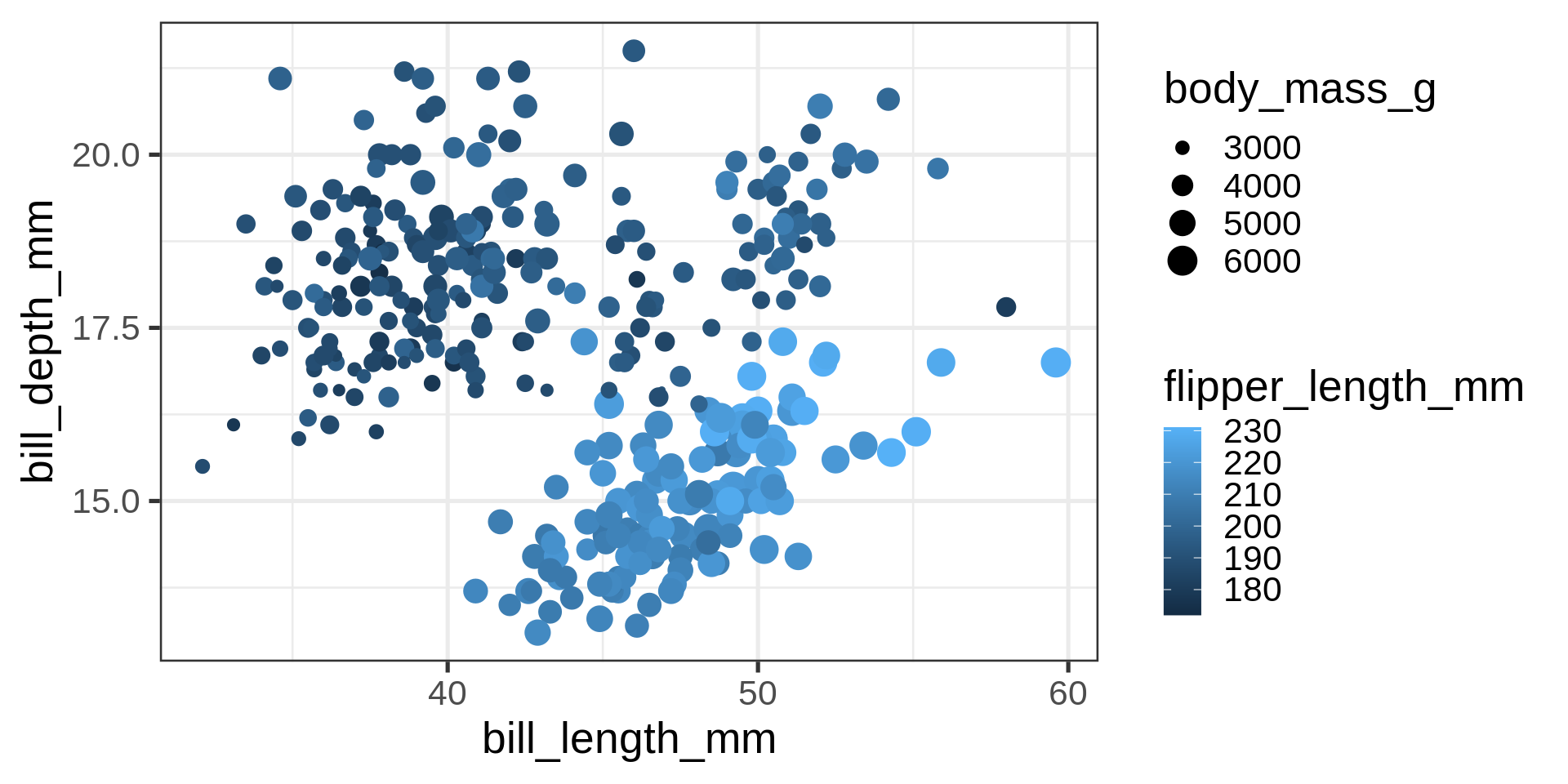
What is the relation between bodymass and bill depth?
Caution
Now four numeric variables. Not a good solution for mapping numeric variables to size and colour for analytical purposes.
Correlograms
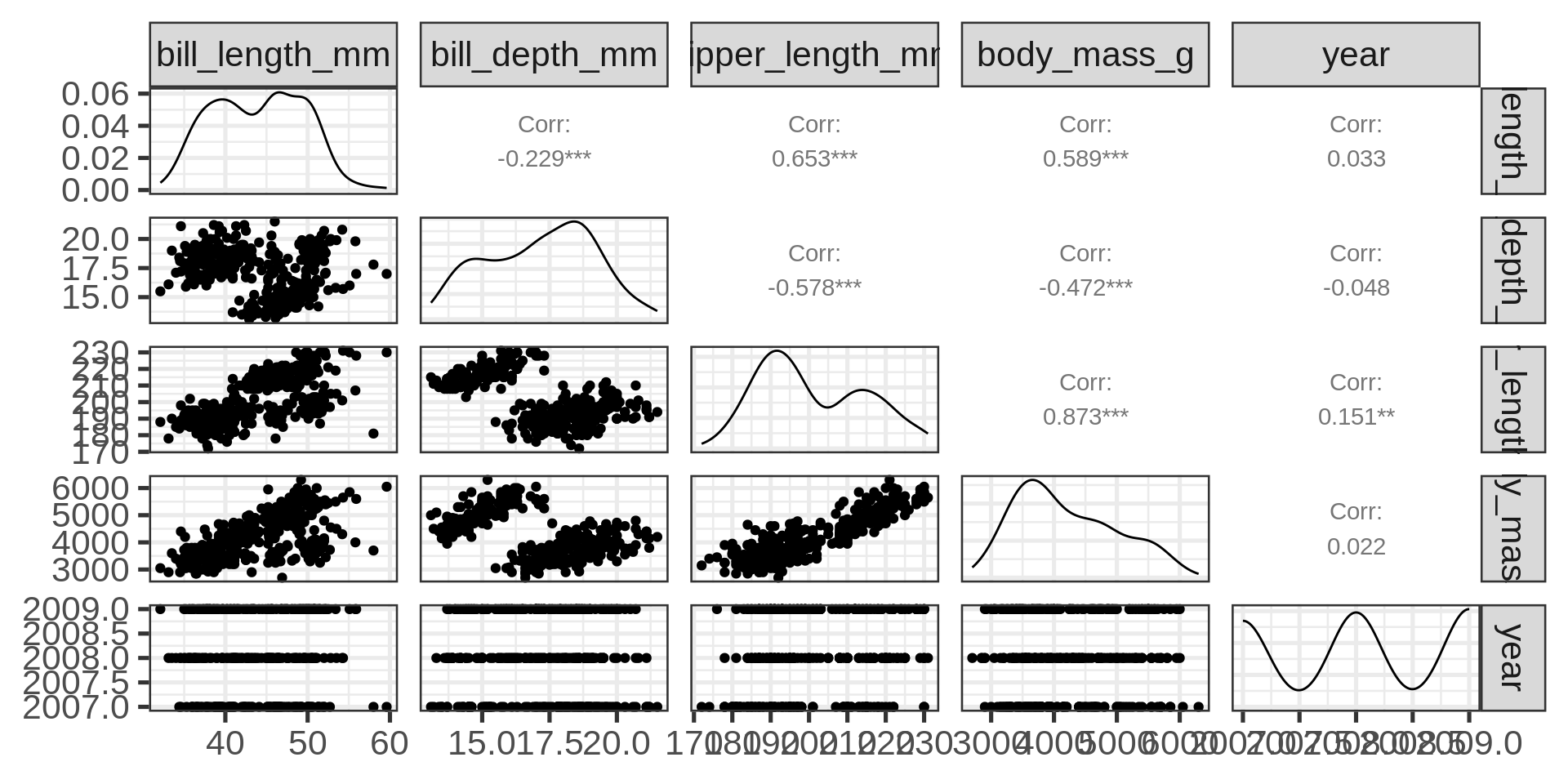
Complete features of GGally::ggpairs()
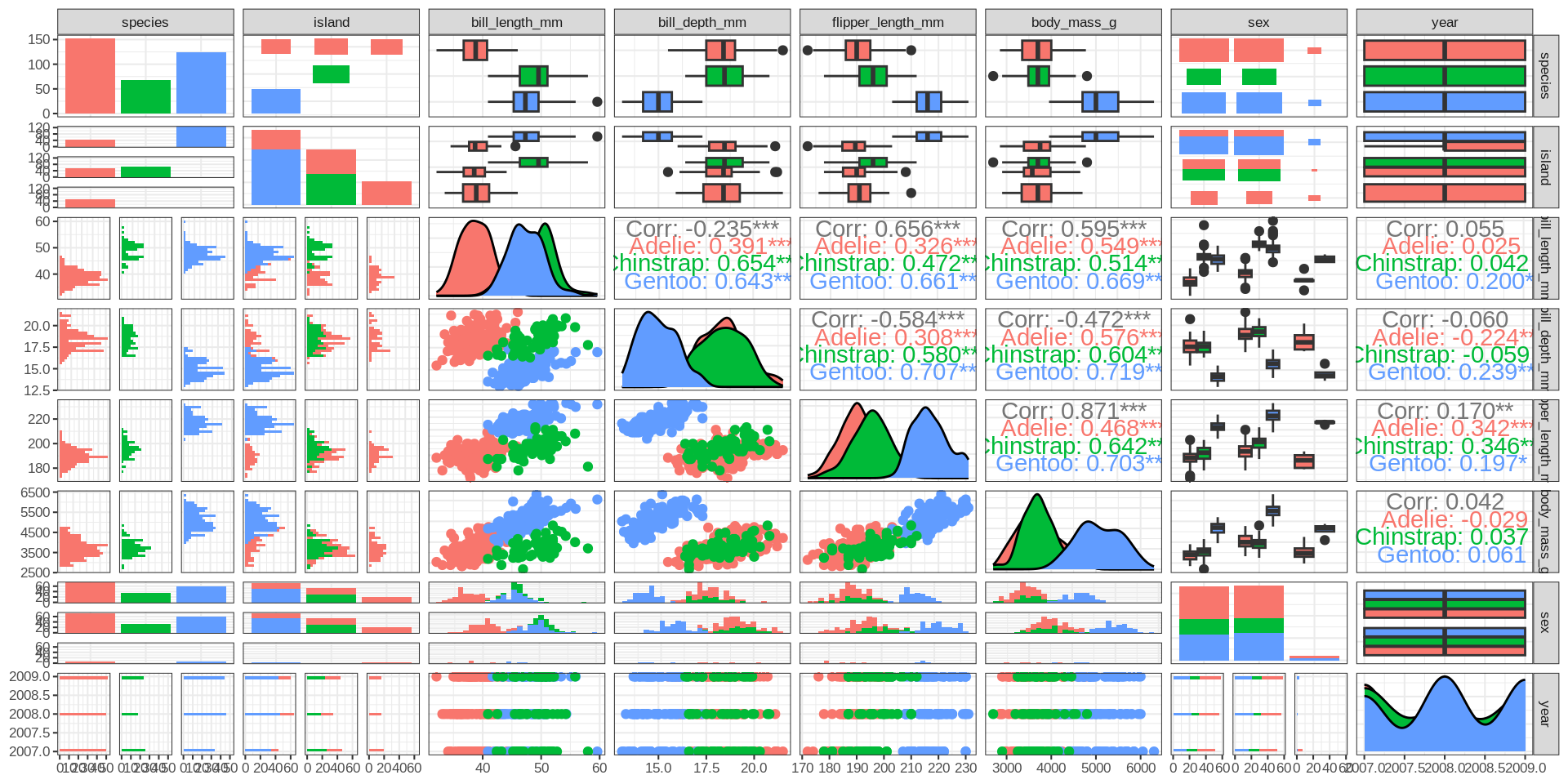
Heatmap
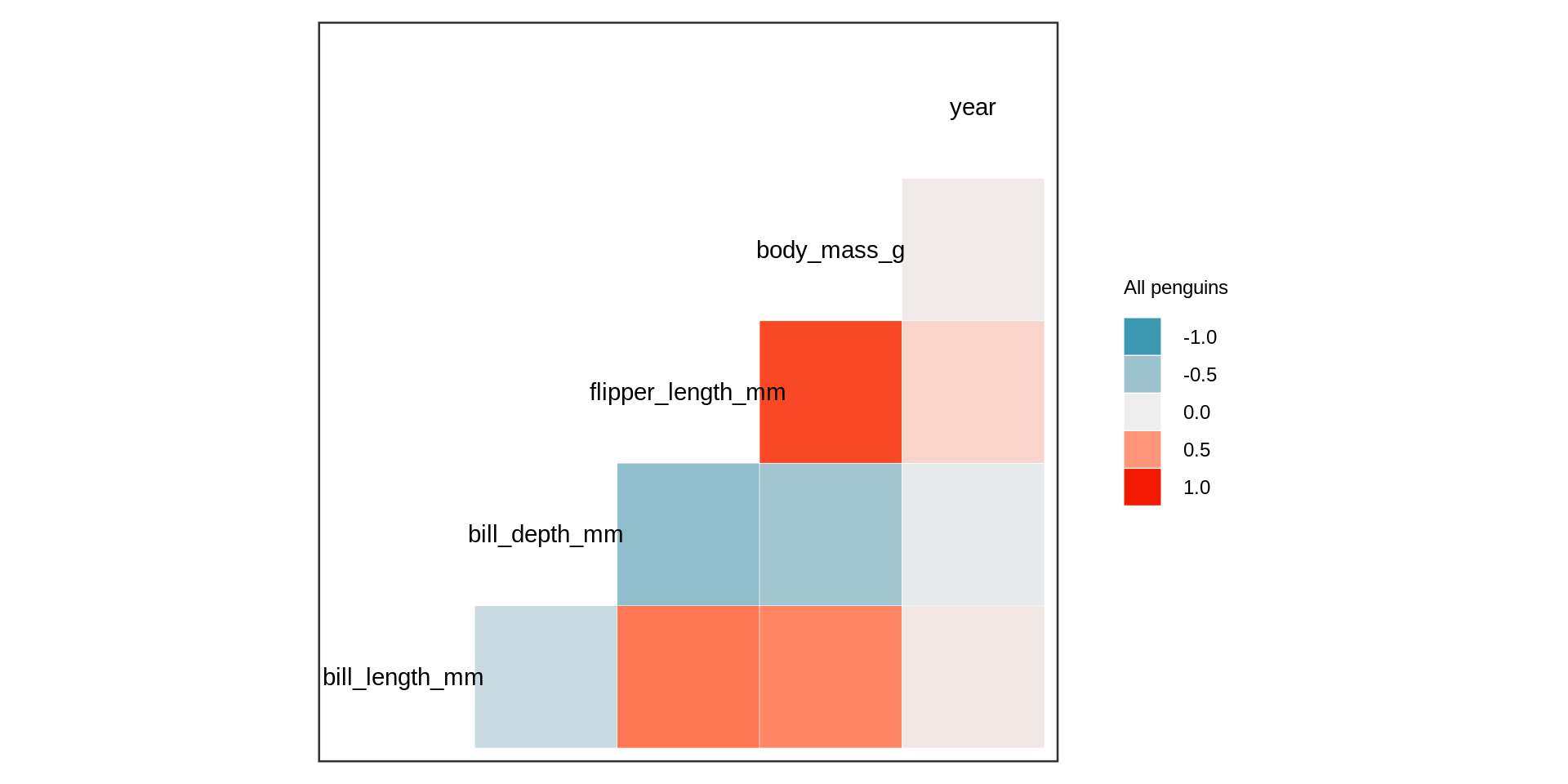
Remember
Simpson paradox
Simpson’s paradox
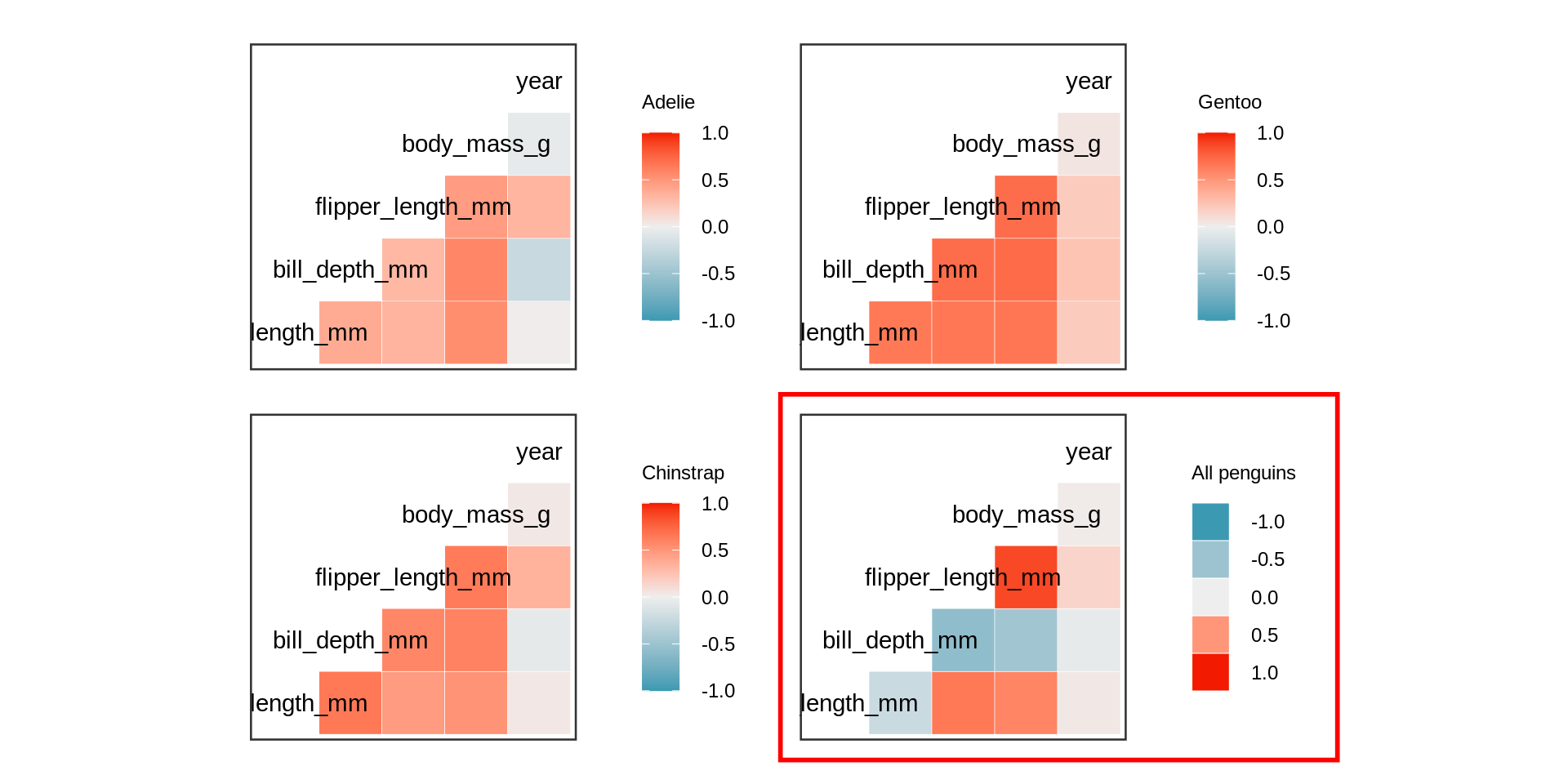
All numeric variables except for year are highly correlated if the individual species are respected.
PCA
Principal component analysis
Dimensionality reduction
With many possibly correlated variables one wants to reduce the number of variables, potentially drop some.
- Standardization/ normalization
- Covariance Matrix
- Eigen Decomposition Calculate eigenvalues (variance explained by components) and eigenvectors (directions of components).
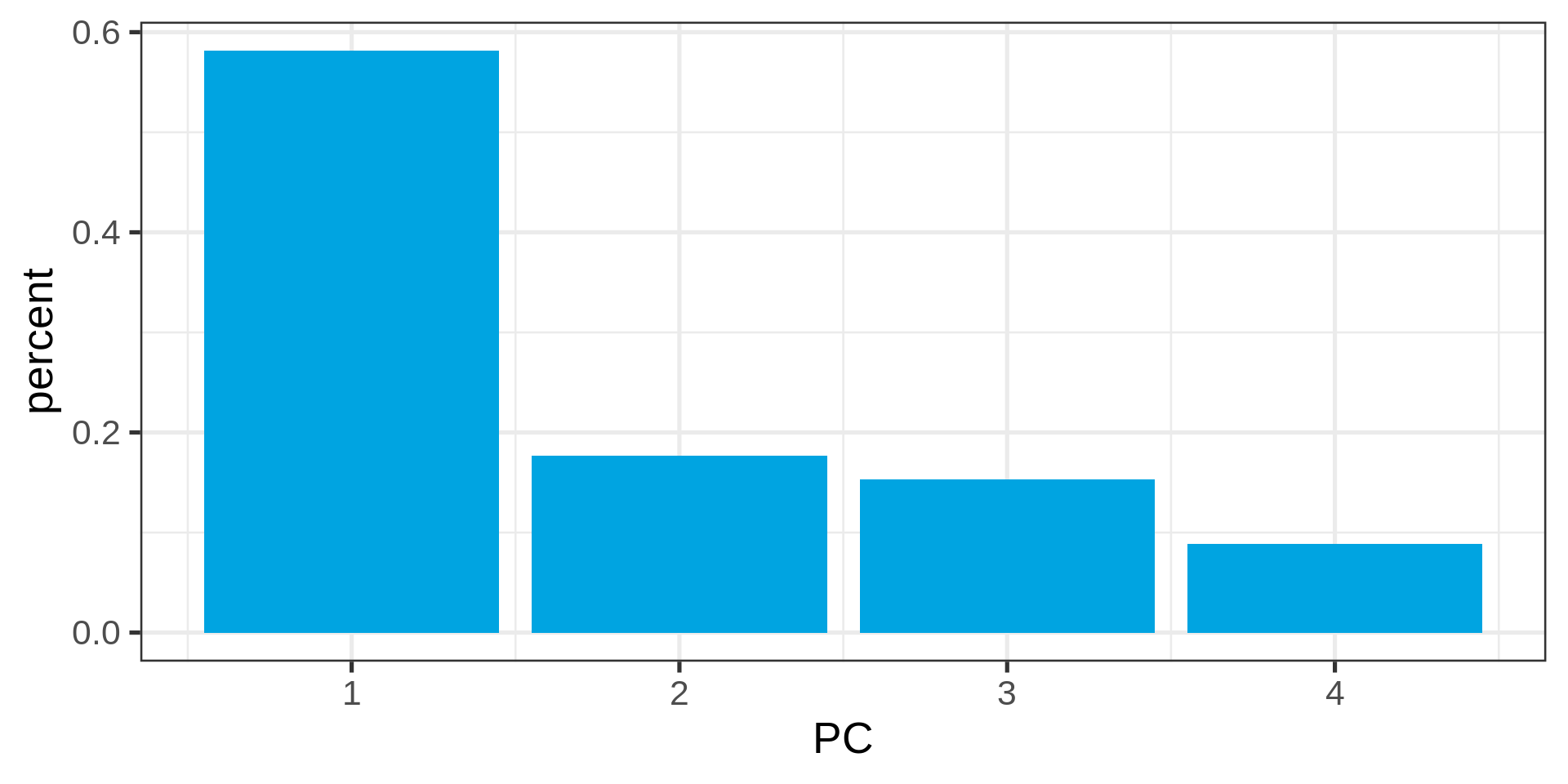
- Select Principal Components: Sort eigenvalues in descending order and select the top \(k\) components.
- Project the original data onto the selected principal components.
Running PCA
Standard deviations (1, .., p=4):
[1] 1.5250081 0.8403736 0.7833863 0.5953389
Rotation (n x k) = (4 x 4):
PC1 PC2 PC3 PC4
bill_length_mm -0.4879448 0.20838845 -0.78794300 0.3124580
bill_depth_mm -0.4944287 0.44731833 0.59986771 0.4422729
flipper_length_mm -0.4382781 -0.86421656 0.12691004 0.2119809
body_mass_g -0.5704055 0.09803219 0.05655442 -0.8135286Principal component analysis in R
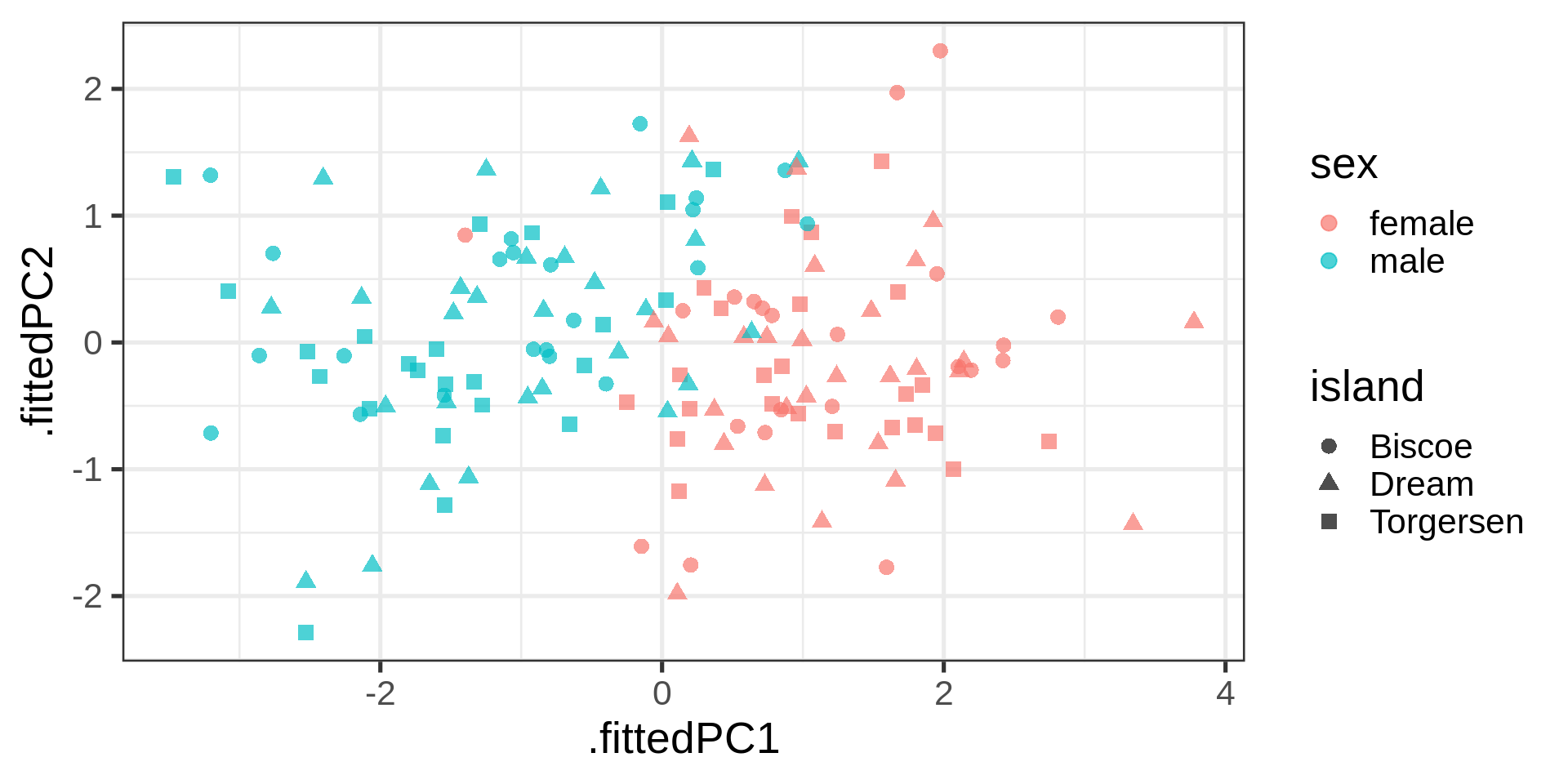
Using Claus Wilke’s suggestion
Loadings
# A tibble: 16 × 3
column PC value
<chr> <dbl> <dbl>
1 bill_length_mm 1 -0.488
2 bill_length_mm 2 0.208
3 bill_length_mm 3 -0.788
4 bill_length_mm 4 0.312
5 bill_depth_mm 1 -0.494
6 bill_depth_mm 2 0.447
7 bill_depth_mm 3 0.600
8 bill_depth_mm 4 0.442
9 flipper_length_mm 1 -0.438
10 flipper_length_mm 2 -0.864
11 flipper_length_mm 3 0.127
12 flipper_length_mm 4 0.212
13 body_mass_g 1 -0.570
14 body_mass_g 2 0.0980
15 body_mass_g 3 0.0566
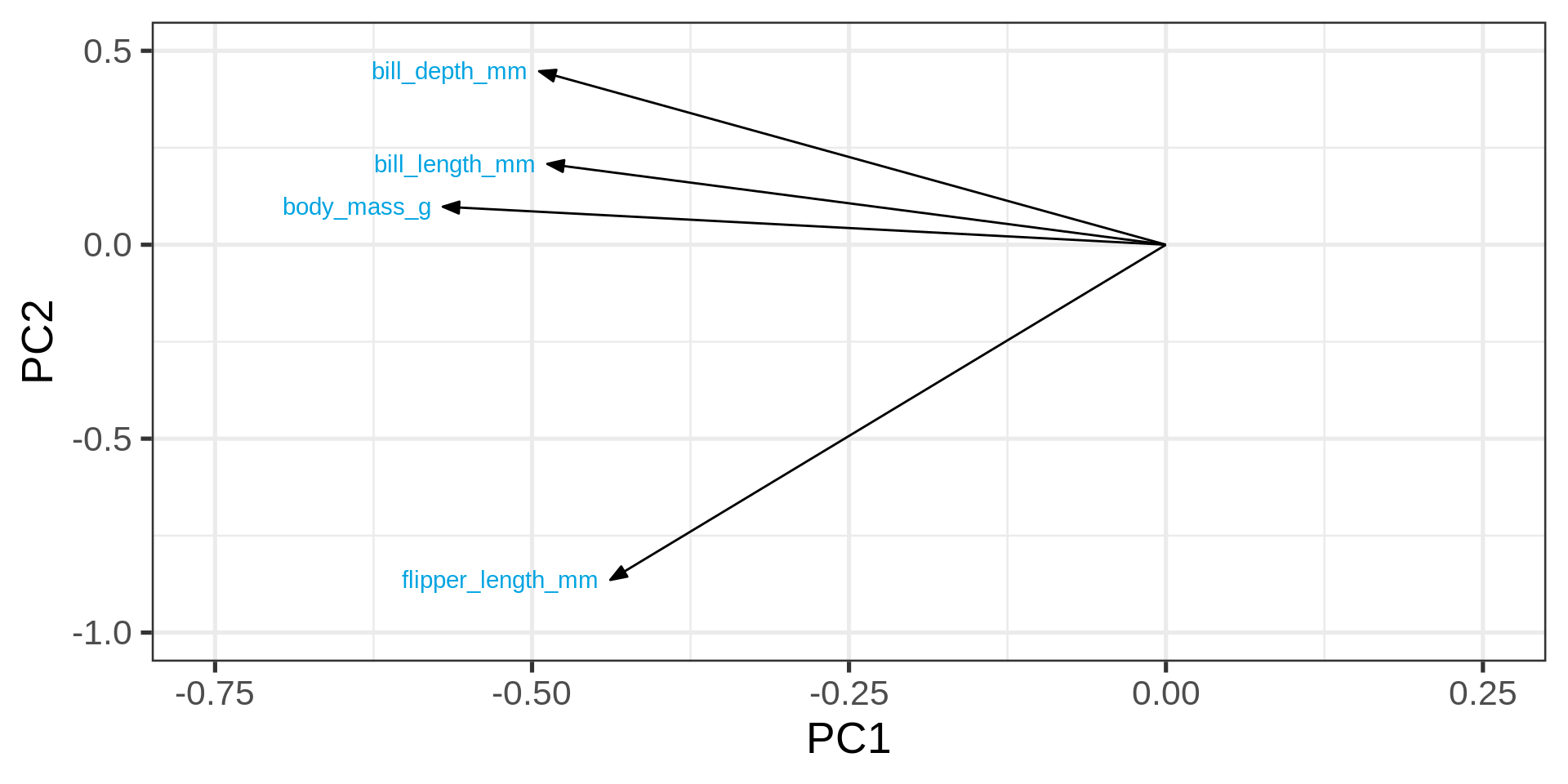
16 body_mass_g 4 -0.814 Plotting the loading
# Nice arrow style
arrow_style <- arrow(
angle = 20,
ends = "first",
type = "closed",
length = grid::unit(8, "pt")
)
# plot rotation matrix
pca |>
tidy(matrix = "rotation") |>
pivot_wider(names_from = "PC", names_prefix = "PC", values_from = "value") |>
ggplot(aes(PC1, PC2)) +
geom_segment(xend = 0, yend = 0, arrow = arrow_style) +
ggrepel::geom_text_repel(
aes(label = column),
hjust = 0.2, nudge_x = -0.05,
color = "#00a4e1"
) +
# Plot padding is often
xlim(-0.75, .25) + ylim(-1, 0.5)